Central and Inscribed Angles in Complex Numbers
This is probably one of the more popular "math facts" that the central angle in a circle is twice the inscribed angle subtended by the same arc. The original formulation comes from Euclid III.20:
In a circle the angle at the center is double the angle at the circumference when the angles have the same circumference as base.
Euclid's proof has been illustrated elsewhere based on the following diagram:
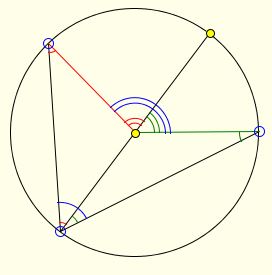
An important corollary of this fact is that, in a circle, all inscribed angles subtended by the same arc are equal. The importance of the statement and the corollary is underscored by the inclusion of a less elementary proof that employs complex numbers in a classic book on advanced geometry of plane curves. Of course, additionally, the proof serves to illustrate basic complex number techniques.
The proof is based on the following diagram.
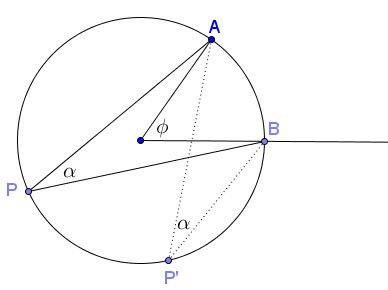
Without loss of generality, the circle is assumed to have radius $1$ and be centered at the origin. The points are identified with complex numbers, so that, say, the equation of the circle is $z=e^{i\psi},$ where $\psi$ is a real number, the angle measured from the horizontal $x\mbox{-axis}.$ Let $B$ correspond to $\psi =0,$ $A$ to $\psi =\phi,$ and $P$ to $\psi =\nu:$ $B=1,$ $A=e^{i\phi},$ $P=e^{i\nu}.$
We find, for vectors, $AP= e^{i\nu}-e^{i\phi},$ $BP= e^{i\nu}-1.$
The argument of the ratio of this two complex numbers is $\angle APB=\alpha.$ Dividing the ratio by its conjugate eliminates the unimportant length of the ratio, but doubles the argument. Thus we have$\displaystyle \begin{align} e^{2i\alpha} &=\frac{e^{i\nu}-e^{i\phi}}{e^{i\nu}-1} : \frac{e^{-i\nu}-e^{-i\phi}}{e^{-i\nu}-1}\\ &=\frac{e^{i\nu}-e^{i\phi}}{e^{i\nu}-1} \cdot \frac{e^{-i\nu}-1}{e^{-i\nu}-e^{-i\phi}}\\ &=\frac{e^{i\nu}-e^{i\phi}}{e^{i\nu}-1} \cdot \frac{e^{i\phi}(1-e^{i\nu})}{e^{i\phi}-e^{i\nu}}\\ &=e^{i\phi}. \end{align}$
Assuming all angles are between $0$ and $\pi,$ $2\alpha=\phi.$
References
- C. Zwikker, The Advanced Geometry of Plane Curves and Their Applications, Dover, 2005, p. 59
Complex Numbers
- Algebraic Structure of Complex Numbers
- Division of Complex Numbers
- Useful Identities Among Complex Numbers
- Useful Inequalities Among Complex Numbers
- Trigonometric Form of Complex Numbers
- Real and Complex Products of Complex Numbers
- Complex Numbers and Geometry
- Central and Inscribed Angles in Complex Numbers
- Plane Isometries As Complex Functions
- Remarks on the History of Complex Numbers
- Complex Numbers: an Interactive Gizmo
- Cartesian Coordinate System
- Fundamental Theorem of Algebra
- Complex Number To a Complex Power May Be Real
- One can't compare two complex numbers
- Riemann Sphere and Möbius Transformation
- Problems
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73601116
