CCC: Gergonnes's Solution to Apollonius' Problem
Each of the cases of the Problem of Apollonius has several known solutions. One of the reasonably standard techniques is to apply inversion, with the idea of getting a simpler configuration, finding a requisite circle, and inverting it back. A solution of the three-circles (CCC) problem by Joseph Diaz Gergonne (1771-1859) is remarkable in that inversion is used as a motivating starting point and subsequently in the proof of the validity of the construction, but not in the construction itself.
Find a circle tangent to three given circles:
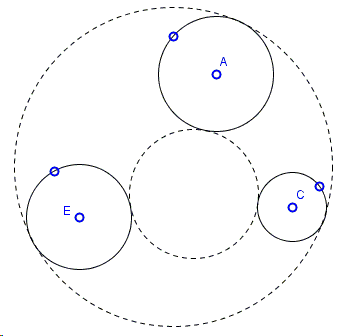
The applet below illustrates Gergonne's construction. The three circles are designated \(A\), \(C\), \(E\) by their centers, and each has a point on the boundary that helps change the circle's radius. Gergonne's construction produces six points \(S_{1}, S_{2}, S_{3}\) and \(T_{1}, T_{2}, T_{3}\) such that the circumcircles \((S_{1}S_{2}S_{3})\) and \((T_{1}T_{2}T_{3})\) serve two (in general out of 8) solutions. However, for some configuration the sets of \(S\) and \(T\) points mix up. The applet is blind to this possibility. The GeoGebra tool makes it easy to sketch various geometric construction but, in order to achieve a perfection, requires study and experience, as would programming directly in a programming language. A Java applet (implementing a different solution) that display a maximum available number of solutions is available elsewhere. Please beware that the applet below suffers from certain limitations.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle tangent to three given circles:

The construction proceeds in several steps:
Step 1: Find a circle \((O)\) orthogonal to all three given circles. This involves finding their radical center \(O\) and the tangents from there to the circles.
Step 2: Find the axis of similitude of the three circles. This is based on Gaspard Monge's theorem and involves drawing common tangents to two circles. (As will be shown later on, the axis of similitude of \(A\), \(C\), \(E\) serves the radical axis of the three coaxal circles \((O)\), \((S_{1}S_{2}S_{3})\), and \((T_{1}T_{2}T_{3}).\)
Step 3: Construct the radical centers \(R,Q,P\) of the triplets of circles \(\{(A),(S_{1}S_{2}S_{3}),(T_{1}T_{2}T_{3})\}\), \(\{(C),(S_{1}S_{2}S_{3}),(T_{1}T_{2}T_{3})\}\), and, respectively, \(\{(E),(S_{1}S_{2}S_{3}),(T_{1}T_{2}T_{3})\}\). E.g., \(P\) is the intersection of \(ST\) - the common chord of \((O)\) and \((E)\) with the axis of similitude from the previous step.
Step 4: Draw tangents from \(R,Q,P\) to \((E)\), \((C)\), and, respectively, \((A)\). This gives points \(S_{1}\), \(T_{1}\) on \((A)\); \(S_{2}\), \(T_{2}\) on \((C)\); \(S_{3}\), \(T_{3}\) on \((E).\)
Step 5: Draw circles \((S_{1}S_{2}S_{3})\) and \((T_{1}T_{2}T_{3}).\)
Why does the construction work?
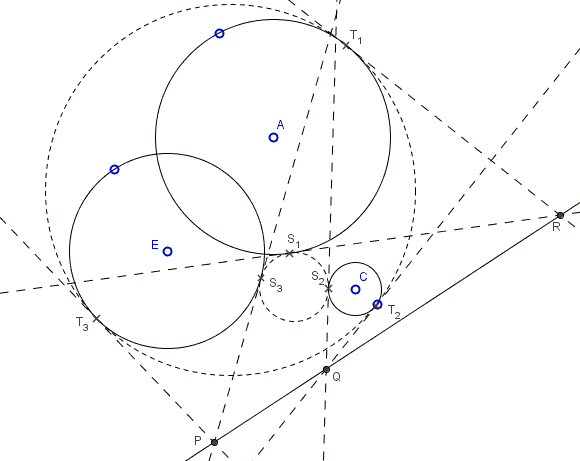
The following points are crucial to the proof:
If the radical center of the three given circles is located outside each of the circles, the tangents from the radical center determine a circle orthogonal to all three.
If there is one solution, say, \((S_{1}S_{2}S_{3})\), there is another one \((T_{1}T_{2}T_{3})\) obtained by inversion in the circle just described - \((O)\) in the construction.
This is due to La Hire's theorem: say, since circles \((E)\) and \((O)\) are orthogonal, line \(S_{3}T_{3}\) passes through \(O\), making \(S_{3}\) and \(T_{3}\) map onto each other by inversion in \((O).\)
The axis of similitude of circles \((A)\), \((C)\), \((E)\) is the radical axis of the pencil of circles that contains \((O)\), \((S_{1}S_{2}S_{3})\) and \((T_{1}T_{2}T_{3}).\)
Indeed (the problem of Four Touching Circles provides a clue), the radical axis of \((S_{1}S_{2}S_{3})\) and \((T_{1}T_{2}T_{3})\) passes through the (external) center of similitude of, say, circles \((A)\) and \((C)\), and also that of the pairs \((A)\), \((E)\) and \((C)\), \((E).\)
(Gergonne's construction in other circle configuration is treated elsewhere.)
References
- J. Casey, A Sequel to the First Six Books of the Elements of Euclid, University of Michigan, 2005 (reprint of 1888 edition), Book VI, Section V, Proposition 10
- J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971, p. 171
- H. Dorrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 1965, 154-159
- J. Hadamard, Lessons in Geometry, AMS, 2008, Complements to Book III, Ch. VI
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73518031
