When A Quadrilateral Is Inscriptible?
For the sake of simplicity, I shall assume throughout that we deal with convex quadrilaterals. If such a quadrilateral ABCD is circumscribed around a circle (a property which is referred to as being inscriptible), then
(1)
AB + CD = BC + AD,
which is easily proven from an observation that two tangents to a circle from a point outside the circle are equal. Thus, (1) is a necessary condition for a (convex) quadrilateral to be inscriptible. Is it sufficient? In other words, given a convex quadrilateral ABCD that satisfies (1), is it inscriptible? Is there a circle that touches all four sides of the quadrilateral? Let us show that this is so:
Any convex quadrilateral that satisfies (1) is inscriptible.
Proof
We start with a construction of a circle tangent to the sides BC, CD, and AD. (The center of the circle is at the intersection of the bisectors of angles C and D.) If the circle is also tangent to AB we are done. So assume to the contrary that the circle is not tangent to AB. Then find AB' tangent to the circle with B' on BC (or its extension).

Since (1) is a necessary condition for a quadrilateral to be inscriptible and AB'CD does possess this property, we have
(1')
AB' + CD = B'C + AD.
Subtracting (1') from (1) and rearranging the terms we obtain
AB - AB' = BC - B'C = BB',
which contradicts the triangle inequality for ΔABB'.
It ought to be mentioned that the diagram drawn does not cover all possible configurations (e.g., it might have happened that AB crossed the constructed circle), but they all are treated in the same way and lead to a triangle that violates the triangle inequality.
Q.E.D.
This is a classical proof by contradiction or, in Latin, reductio ad absurdum: An assumption that a property holds (or does not hold) leads to a contradiction, therefore the opposite to the assumption must be true.
Looks like we are done and it is time to turn our attention to another interesting topic. However, the proof just given has a flaw that, in principle, may be repaired, but at a considerable effort.
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
The problem with the above proof is in the tacit assumption that the circle touches AD somewhere between A and D. As far as the premises of the theorem go, this fact is not immediately obvious. However, if the point of tangency is outside the segment AD, the whole construction breaks down (especially if it is on the side of A.)
As a replacement, consider the following entirely different approach. However note that a slight conceptual modification of the previous proof in interpreting the symbols in the derivation renders the proof absolutely valid.
First note that any kite is inscriptible, so we may assume that the given quadrilateral ABCD is not a kite. Thus either
If
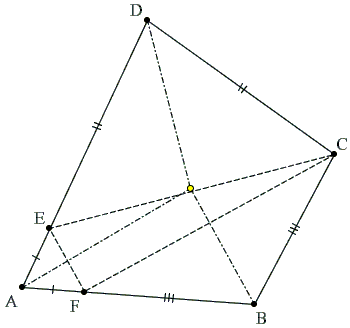
We can rewrite (1) as
AF + BF + CD = AE + DE + BC.
Taking into account DE = CD and
AF = AE.
We now see that the three triangles CBF, EDC, and FAE are isosceles. In every isosceles triangle the bisector of the angle at the apex serves as the perpendicular bisector of the base. It follows that the bisectors of the angles at B, A, and D are simultaneously the perpendicular bisectors of the sides of ΔCEF and are, therefore, concurrent. Their common point is equidistant from all four sides of quadrilateral ABCD which leads to the required conclusion that ABCD is inscriptible.
([Andreescu and Enescu, pp. 65-67] gives both proofs without mentioning the flaw in the first one. [Fetisov], on the other hand, makes a point of it.)
References
- N. Altshiller-Court, College Geometry, Dover, 1980
- T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004
- A. I. Fetisov, Ya. S. Dubnov, Proof in Geometry: With "Mistakes in Geometric Proofs", Dover, (December 25) 2006
Inscriptible (tangential, circumscribed) Quadrilateral
- When A Quadrilateral Is Inscriptible?
- Inscriptible Quadrilateral: An Illustration
- Inscriptible and Exscriptible Quadrilaterals
- Pairs of Incircles in a Quadrilateral
- Butterfly in Inscriptible Quadrilateral
- Inscriptible Quadrilateral of Triangle Incenters
- Perpendicular Bisectors in an Inscriptible Quadrilateral II
- A Property of Inscriptible Quadrilaterals
- An Inradii Relation in Inscriptible Quadrilateral
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
Darij Grinberg made the following observation:
... the proof above is not as wrong as suggested. What can indeed be said to its disadvantage is that it is incomplete in the very way it is written - but this is the case for many geometric proofs, alas - and that it is not as vivid as it looks. But with some knowledge of directed lines and directed circles, this can be helped in a straightforward way. In fact, one has to first prove the necessity of the condition (that ABCD being circumscribed implies
Let a, b, c, d be four directed lines all touching one directed circle. (Directed objects are said to touch each other if they touch each other as non-directed objects, and their directions at the point of tangency coincide.) Let
Once this is proven, the sufficiency follows easily using your "flawed" argument. Whether the circle touches AD between A and D or somewhere far beyond A is not of matter anymore - it just determines whether the quadrilateral ABCD is convex or self-intersecting and has an incircle or an excircle, what is all the same from the viewpoint of directed lines touching directed circles...
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73581240
