An Inradii Relation in Inscriptible Quadrilateral
Introduction
The statement below that expresses the inradius of an inscriptible (also tangential, circumscribed) quadrilateral $ABCD\;$ with the inradii of triangles $ABC,\;$ $BCD,\;$ $CDA,\;$ and $DAB,\;$ is the invention of Borislav Mirchev (Bulgaria). Borislav posted the problem of finding such a relationship on several forums and collected the results. He passed his collection of four proofs to me, for which I am very much in his debt.
The first two proofs are due to Israel Diaz Acha (Peru), the third to Borislav himself; the fourth solution was found on the Russian discussion forum https://dxdy.ru/, posted by the user under the nickname mihiv.
Problem
Given an inscriptible quadrilateral $ABCD,\;$ with inradius $r.\;$ Consider triangles $ABC,\;$ $BCD,\;$ $CDA,\;$ and $DAB,\;$ and denote their inradii $r_1,\;$ $r_2,\;$ $r_3,\;$ $r_4.$
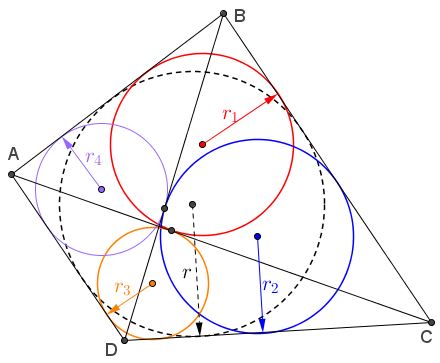
Let's denote
$F=r_1r_3+r_2r_4,\\ G=r_1r_2r_3+r_2r_3r_4+r_3r_4r_1+r_4r_1r_2,\\ H=r_1r_2r_3r_4.\;$
Prove that
$\displaystyle r=\frac{G+\sqrt{G^2-4H\cdot F}}{2F}.$
Solution 1
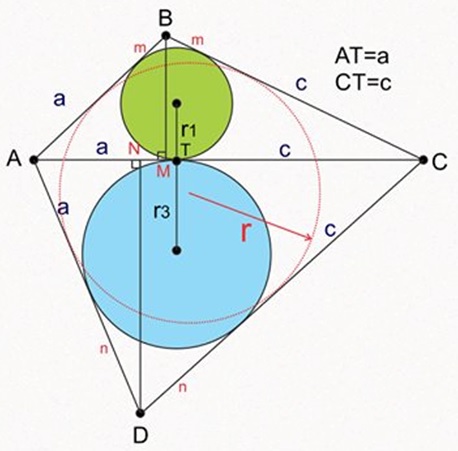
$\displaystyle r_1=\sqrt{\frac{acm}{a+c+m}},\;$ implying $\displaystyle m=\frac{\left(a+c\right)r_1^2}{ac-r_1^2}.\;$ $\displaystyle r_3=\sqrt{\frac{acn}{a+c+n}}\;$ so that $\displaystyle n=\frac{\left(a+c\right)r_3^2}{ac-r_3^2}.\;$ $\displaystyle r=\frac{\left(a+c+m\right)r_1+\left(a+c+n\right)r_3}{a+c+m+n}.$
From these three equations it follows successively that: $\displaystyle r=\frac{ac\left(r_1+r_3\right)}{ac+r_1r_3},\;$ $\displaystyle ac=\frac{rr_1r_3}{r_1+r_3-r},\;$ $\displaystyle BM=\frac{2acr_1}{ac-r_1^2},\;$ $\displaystyle DN=\frac{2acr_3}{ac-r_3^2};\;$ $\displaystyle CM=\frac{a+c}{2}+\frac{c-a}{c+a}\left(\frac{c+a+2m}{2}\right),\;$ $\displaystyle CN=\frac{a+c}{2}+\frac{c-a}{c+a}\left(\frac{c+a+2n}{2}\right).\;$
Thus, $BD^2=\left(BM+DN\right)^2+\left(CM+CN\right)^2.$
By analogy: $\displaystyle BX\cdot XD=\frac{rr_2r_4}{r_2+r_4-r}.\;$ But $4BX\cdot XD=BD^2-\left(CB-CD\right)^2=BD^2-\left(m-n\right)^2.\;$
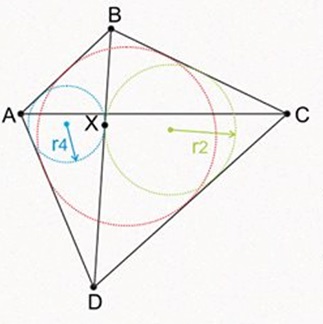
Replacing:
$\displaystyle\begin{align} 4BX\cdot XD &=\left(\frac{2acr_1}{ac-r_1^2}+\frac{2acr_3}{ac-r_3^2}\right)^2+\left(\frac{c-a}{c+a}\right)^2\left(m-n\right)^2-\left(m-n\right)^2\\ &=4\left(ac\right)^2\left(\frac{acr_1}{ac-r_1^2}+\frac{acr_3}{ac-r_3^2}\right)^2-4\left(ac\right)^3\left(\frac{1}{ac-r_1^2}-\frac{1}{ac-r_3^2}\right) \end{align}$
from which
$\displaystyle\begin{align} BX\cdot XD &= \left(\frac{ac\left(r_1+r_3\right)}{\left(ac-r_1^2\right)\left(ac-r_3^2\right)}\right)^2\left[\left(ac-r_1r_3\right)^2-ac\left(r_1-r_3\right)^2\right]\\ &=\frac{a^2c^2\left(r_1+r_3\right)^2}{\left(ac-r_1^2\right)\left(ac-r_3^2\right)}. \end{align}$
Now replacing $\displaystyle ac=\frac{rr_1r_3}{r_1+r_3-r}\;$ we have
$\displaystyle BX\cdot XD=\frac{r^2r_1r_3}{\left(r-r_1\right)\left(r-r_3\right)}=\frac{rr_2r_4}{r_2+r_4-r}$
from which, successively,
$\displaystyle r^2\left(r_1r_3+r_2r_4\right)-r\left(r_1r_3\left(r_2+r_4\right)+r_2r_4\left(r_1+r_3\right)\right)+r_1r_2r_3r_4=0,\\ \displaystyle \frac{\left(r-r_1\right)\left(r-r_3\right)}{r_1r_3}+\frac{\left(r-r_2\right)\left(r-r_4\right)}{r_2r_4}=1,$
or
$\displaystyle r=\frac{G+\sqrt{G^2-4H\cdot F}}{2F}.$
Solution 2
$\displaystyle\frac{(r-r_1)(r-r_3)}{r_1r_3}=\frac{\cos (\frac{B-D}{2})-\cos (\frac{B+D}{2})}{\cos (\frac{B-D}{2})+\cos (\frac{A-C}{2})}.$
Since $\displaystyle r=\frac{ac(r_1+r_3)}{ac+r_1r_3}$ (see Solution 1 for proof), replacing we have:
(*)
$\displaystyle\frac{(r-r_1)(r-r_3)}{r_1r_3}=\frac{(ac-r_1^2)(ac-r_3^2)}{(ac+r_1r_3)^2}.$
We have: $a=r_1\cot x=r_3\cot z$ and $c=r_1\cot y=r_3\cot w.$
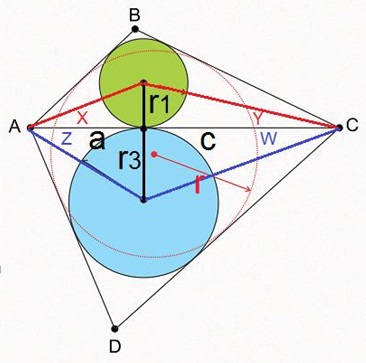
Replacing in (*) we obtain:
(**)
For the angles we have the following relations: $\displaystyle x+y=90^{\circ}-\frac{B}{2}$; $\displaystyle z+w=90^{\circ}-\frac{D}{2}$; $\displaystyle x+z=\frac{A}{2}$; $\displaystyle x+z=\frac{C}{2}.$ Replacing in (**) we obtain:
$\displaystyle\frac{\cos (180^{\circ}-\frac{B+D}{2}) + \cos (\frac{B+D}{2}) }{\cos (\frac{A-C}{2})+\cos (\frac{D-B}{2})}=\frac{\cos (\frac{D-B}{2})-\cos (\frac{D+B}{2}) }{\cos (\frac{A-C}{2})+\cos (\frac{D-B}{2})}.$
By analogy it can be proven that: $\displaystyle \frac{(r-r_2)(r-r_4)}{r_2r_4}=\frac{\cos (\frac{A-C}{2})-\cos (\frac{A+C}{2})}{\cos (\frac{A-C}{2})+\cos (\frac{B+D}{2})}.$
But we have: $\displaystyle\cos \frac{B+D}{2}+\cos \frac{A+C}{2}=0,\;$ so it follows that: $\displaystyle\frac{(r-r_1)(r-r_3)}{r_1r_3}+\frac{(r-r_2)(r-r_4)}{r_2r_4}=1.$
From the last equation it follows that:
$\displaystyle r=\frac{G+\sqrt{G^2-4H\cdot F}}{2F}.$
Solution 3
Let the tangents from the vertices $A,\;$ $B,\;$ $C,\;$ $D$ to the quadrilateral's incircle (having radius $r$) are with lengths $a,$ $b,$ $c,$ $d.$ According to Lemma 3 from Forum Geometricorum it follows that $\displaystyle u^2=\frac{a+c}{b+d}((a+c)(b+d)+4bd)$ and $\displaystyle v^2=\frac{b+d}{a+c}((a+c)(b+d)+4ac),$ where $AC=u$ and $BD=v.$
Let $I$ and $I'$ be the incenters of the circles inscribed in $ABCD$ and $ABC.$ It follows that $I'$ lies on the angle bisector $BI.$ Let $T$ and $T'$ are the tangency points of the $ABCD$'s incircle and $ABC$'s incircle with $AB.$ It follows that the $\triangle{BIT} \sim \triangle{BI'T'},$ implying $\displaystyle \frac{IT}{I'T'}=\frac{BT}{BT'},$ so that $\displaystyle \frac{r}{r_{ABC}}=\frac{2b}{a+b+b+c-u}\;$ or $\displaystyle r_1=\frac{(a+b+b+c-u)u}{2b}.\;$ By analogy, we obtain similar equations for $r_2,$ $r_3,$ $r_4.$
Thus we have the following simultaneous equations:
(1)
$\displaystyle r_1=\frac{(a+b+b+c-u)r}{2b}$
(2)
$\displaystyle r_3=\frac{(a+d+d+c-u)r}{2d}$
(3)
$\displaystyle r_2=\frac{(b+c+c+d-v)r}{2c}$
(4)
$\displaystyle r_4=\frac{(b+a+a+d-v)r}{2a}$
(5)
$\displaystyle u^2=\frac{a+c}{b+d}((a+c)(b+d)+4bd)$
(6)
$\displaystyle v^2=\frac{b+d}{a+c}((a+c)(b+d)+4ac)$
We may rewrite (1) as
(1')
$\displaystyle \frac{r_1-r}{r}=\frac{a+c-u}{2b}$
and (2) as
(2')
$\displaystyle \frac{r_3-r}{r}=\frac{a+c-u}{2d}$
Summing (1') and (2') we obtain:
(3')
$\displaystyle \frac{r_1+r_3-2r}{r}=(a+c-u)\frac{b+d}{2bd},$
implying $\displaystyle u-a-c=\frac{2b}{b+d}\cdot\frac{2r-r_1-r_3}{r}$
From (5) we have:
(5')
$\displaystyle (u+a+c)(u-a-c)=(a+c)\frac{4bd}{b+d}$
Replacing from (3') in (5') we have $\displaystyle u+a+c=2(a+c)\cdot\frac{r}{2r-r_1-r_3},$ i.e.,
(*)
$\displaystyle u=(a+c)\cdot\frac{r_1+r_3}{2r-r_1-r_3}$
After replacing $u$ from (*) in (1) we have $\displaystyle \frac{r-r_1}{r}=\frac{r_1+r_2-r}{2r-r_1-r_2}\cdot\frac{a+c}{b},$ or
(**)
$\displaystyle \frac{b}{a+c}=\frac{r_1+r_2-r}{2r-r_1-r_2}\cdot\frac{r}{r-r_1}.$
Replacing $u$ from (*) in (2) we have $\displaystyle \frac{r-r_2}{r}=\frac{r_1+r_2-r}{2r-r_1-r_2}\cdot\frac{a+c}{d},$ which gives
(***)
$\displaystyle \frac{d}{a+c}=\frac{r_1+r_2-r}{2r-r_1-r_2}\cdot\frac{r}{r-r_2}.$
Summing (**) and (***) obtain:
(I)
$\displaystyle \frac{(r_1+r_2-r)r}{(r-r_1)(2r-r_1-r_2)}+\frac{(r_1+r_2-r)r}{(r-r_2)(2r-r_1-r_2)}=\frac{b+d}{a+c}$
In a similar way from the equations (3), (4), (6) obtain:
(II)
$\displaystyle\frac {(r_3+r_4-r)r}{(r-r_3)(r-r_4)}=\frac{a+c}{b+d}$
From (I) and (II) it follows that
$r^2(r_1r_3+r_2r_4)-r(r_1r_2r_3+r_2r_3r_4+r_3r_4r_1+r_4r_1r_2)+r_1r_2r_3r_4=0$
which implies
(III)
$\displaystyle r_{-}=\frac{G-\sqrt{G^2-4H\cdot F}}{2F}.$
and
(III')
$\displaystyle r_{+}=\frac{G+\sqrt{G^2-4H\cdot F}}{2F}.$
From equation (5) it follows that $u\gt a+c.$ From equations (1') and (2') it follows that $r\gt r_1,$ $r\gt r_3.$
From equation (6) it follows that $v\gt a+c.$ And thus in a similar way we have $r\gt r_2$ and $r\gt r_4.$ Thus:
(IV)
$\displaystyle\frac {r_1+r_2+r_3+r_4}{2}<2r_{-}$
After multiplying the numerator and the denominator of
$\displaystyle \frac{G-\sqrt{G^2-4H\cdot F}}{2F}.$
by $G+\sqrt{G^2-4H\cdot F}\;$ we obtain that
$2r_{-}\cdot (G+\sqrt{G^2-4H\cdot F})=H$
which implies
$\displaystyle\begin{align} 8H &\lt\frac{(r_1+r_2+r_3+r_4)G}{2}\\ &\lt 2r_{-}\cdot (G+\sqrt{G^2-4H\cdot F})\\ &=4H \end{align}$
and, therefore, $4H<0,$ but this is impossible since $r_1, r_2, r_3, r_4\;$ are positive. So we conclude that $r_{-}\;$ is not a solution to our problem, but $r_{+}\;$ is. Therefore,
$\displaystyle r=r_{+}=\frac{G+\sqrt{G^2-4H\cdot F}}{2F}.$
The expression under the square root is always positive:
$\begin{align} D&=G^2-4H\cdot F\\ &=(r_1r_2r_3+r_2r_3r_4+r_3r_4r_1+r_4r_1r_2)^2-4r_1r_2r_3r_4(r_1r_3+r_2r_4)\\ &=r_1^2r_2^2r_3^2+2r_1^2r_2^2r_3r_4+r_1^2r_2^2r_4^2+2r_1^2r_2r_3^2r_4+2r_1^2r_2r_3r_4^2+r_1^2r_3^2r_4^2\\ &\qquad +2r_1r_2^2r_3^2r_4+2r_1r_2^2r_3r_4^2+2r_1r_2r_3^2r_4^2+r_2^2r_3^2r_4^2-4r_1^2r_2r_3^2r_4-4r_1r_2^2r_3r_4^2\\ &=r_1^2r_2^2r_3^2+2r_1^2r_2^2r_3r_4+r_1^2r_2^2r_4^2-2r_1^2r_2r_3^2r_4+2r_1^2r_2r_3r_4^2+r_1^2r_3^2r_4^2\\ &\qquad +2r_1r_2^2r_3^2r_4-2r_1r_2^2r_3r_4^2+2r_1r_2r_3^2r_4^2+r_2^2r_3^2r_4^2\\ &\gt (r_1^2r_2^2r_3^2-2r_1^2r_2r_3^2r_4+r_1^2r_3^2r_4^2)+(r_1^2r_2^2r_4^2-2r_1r_2^2r_3r_4^2+r_2^2r_3^2r_4^2)\\ &\ge 0. \end{align}$
Solution 4
Quadrilateral's perimeter: $p=2r\Sigma ,\;$ where $\displaystyle\Sigma=\cot \frac A2+\cot \frac B2+\cot \frac C2+\cot \frac D2.\;$ From here the area of the quadrilateral:
(1)
$S=\frac 12pr=r^2\Sigma.$
In triangles $ABC$ and $ACD$ we find:
$\displaystyle AB+BC-AC=2r_1\cot \frac B2,\\ \displaystyle AD+CD-AC=2r_3\cot \frac D2$
and it follows that
(2)
$\displaystyle AC=\dfrac p2-\left(r_1\cot \frac B2+r_3\cot \frac D2\right).$
By analogy, in triangles $ABD$ and $BCD$ we find: $\displaystyle BD=\dfrac p2-\left(r_2\cot \frac C2+r_4\cot \frac A2\right).$
Next, we find triangles' perimeters. With (2) in mind, $\displaystyle p_1=(AB+BC-AC)+2AC=p-2r_3\cot \frac D2.$ In this way we obtain: $\displaystyle p_3=p-2r_1\cot \frac B2,\;$ $\displaystyle p_2=p-2r_4\cot \frac A2,\;$ $\displaystyle p_4=p-2r_2\cot \frac C2.$
Express the area $S\;$ in two ways:
$\displaystyle S=S_{ABC}+S_{ACD}=\frac 12(p_1r_1+p_3r_3)=\frac 12(r_1+r_3)p-r_1r_3\left(\cot \frac B2+\cot \frac D2\right)$
and
$\displaystyle S=S_{ABD}+S_{BCD}=\frac 12(p_2r_2+p_4r_4)=\frac12(r_2+r_4)p-r_2r_4\left(\cot \frac A2+\cot \frac C2\right)$
Multiplying the first equation by $r_2r_4,$ and the second by $r_1r_3,$ and adding up, we get: $FS=(rG-H)\Sigma .\;$ Substituting $\Sigma\;$ from (1), we have for $r$ a second degree equation: $Fr^2-Gr+H=0.$
Inscriptible (tangential, circumscribed) Quadrilateral
- When A Quadrilateral Is Inscriptible?
- Inscriptible Quadrilateral: An Illustration
- Inscriptible and Exscriptible Quadrilaterals
- Pairs of Incircles in a Quadrilateral
- Butterfly in Inscriptible Quadrilateral
- Inscriptible Quadrilateral of Triangle Incenters
- Perpendicular Bisectors in an Inscriptible Quadrilateral II
- A Property of Inscriptible Quadrilaterals
- An Inradii Relation in Inscriptible Quadrilateral
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73566304
