Inscriptible Quadrilateral of Triangle Incenters
What Might This Be About?
Problem
Given inscriptible quadrilateral $ABCD,$ construct four squares $AFGB,$ $BLXC,$ $CJKD,$ $DHIA$ (all either outer or inner, relative to the quadrilateral). Let $N,$ $M,$ $P,$ $Q$ be the incenters of triangles $BGL,$ $XCJ,$ $KDH,$ $IAF,$ respectively.
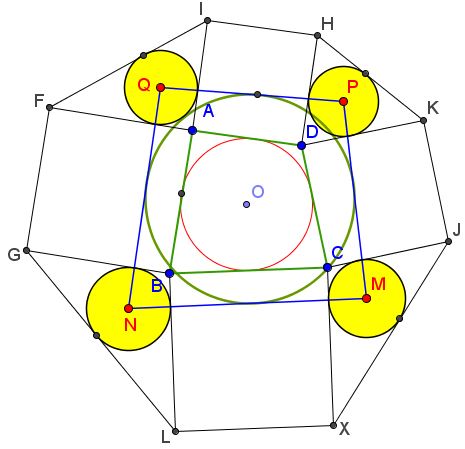
Then $MNPQ$ is an inscriptible quadrilateral.
Solution
Solution is wanting.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
Inscriptible (tangential, circumscribed) Quadrilateral
- When A Quadrilateral Is Inscriptible?
- Inscriptible Quadrilateral: An Illustration
- Inscriptible and Exscriptible Quadrilaterals
- Pairs of Incircles in a Quadrilateral
- Butterfly in Inscriptible Quadrilateral
- Inscriptible Quadrilateral of Triangle Incenters
- Perpendicular Bisectors in an Inscriptible Quadrilateral II
- A Property of Inscriptible Quadrilaterals
- An Inradii Relation in Inscriptible Quadrilateral
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580528
