A Property of Inscriptible Quadrilaterals
Source
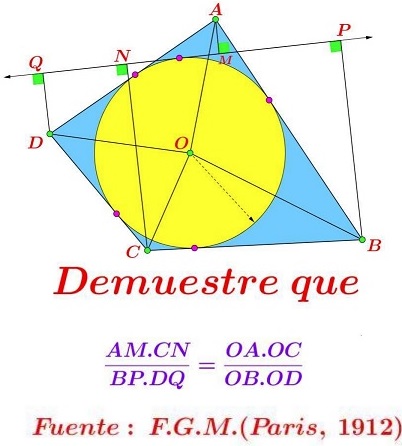
Problem
$(O)\;$ is the incircle of an inscriptible quadrilateral $ABCD.\;$ Line $\ell\;$ is tangent to $(O).\;$ Let $a,b,c,d\;$ be the distances from the vertices $A,B,C,D\;$ to $\ell.$
Then $\displaystyle\frac{ac}{bd} = \frac{AO\cdot CO}{BO\cdot DO}.$
Proof 1
Choose $(O)\;$ $x^2+y^2=1\;$ and $\displaystyle A=\left(1,\frac{\sin t}{\cos t}\right),\;$ $\displaystyle B=\left(\frac{\cos (u+t)}{\cos (u-t)},\frac{\sin (u+t)}{\sin (u-t)}\right),\;$ $\displaystyle C=\left(\frac{\cos (u+v)}{\cos (u-v)},\frac{\sin (u+v)}{\sin (u-v)}\right),\;$ $\displaystyle D=\left(1,\frac{\sin v}{\cos v}\right),\;$ with $0\lt t\lt u\lt v\lt\pi\;$ and $\displaystyle t\lt\frac{\pi}{2},\;$ $\displaystyle u-t\lt\frac{\pi}{2},\;$ $\displaystyle v-u\lt\frac{\pi}{2},\;$ $\displaystyle v\gt\frac{\pi}{2}.\;$
WLOG, $\ell\;$ is defined by $x\cos 2\alpha +y\sin 2\alpha =1,\;$ $0\lt\alpha\lt t.\;$ We get
$\displaystyle\begin{align} a&=\left|\cos 2\alpha+\frac{\sin t\sin 2\alpha}{\cos t}-1\right|\\ &=\left|\frac{\cos (t- 2\alpha)}{\cos t}-1\right|\\ &=\frac{2\sin\alpha\sin (t-\alpha)}{\cos t}. \end{align}$
Similarly, $\displaystyle d=-\frac{2\sin\alpha\sin (v-\alpha)}{\cos v}.\;$ Also,
$\displaystyle\begin{align} b&=\left|\frac{\cos (u+t)\cos 2\alpha}{\cos (u-t)}+\frac{\sin (u+t)\sin 2\alpha}{\cos (u-t)}-1\right|\\ &=\left|\frac{\cos (u+t- 2\alpha)}{\cos (u-t)}-1\right|\\ &=\frac{2\sin (u-\alpha)\sin (v-\alpha)}{\cos (u-t)}. \end{align}$
Similarly, $\displaystyle c=\frac{2\sin (u-\alpha)\sin (v-\alpha)}{\cos (v-u)}.\;$ From here
$\displaystyle\frac{ac}{bd}=-\frac{cos v\cos (u-t)}{\cos t\cos (v-u)}.$
It is easy to see that $\displaystyle\frac{AO\cdot CO}{BO\cdot DO}=-\frac{cos v\cos (u-t)}{\cos t\cos (v-u)}$ and this completes the proof.
Proof 2
Let $E,F\;$ be the points of intersection of $\ell\;$ with $AB\;$ and $CD,\;$ respectively. And denote the angles of the quadrilateral $ABCD\;$ $2\alpha,\;$ $2\beta,\;$ $2\gamma,\;$ $2\delta,\;$ and the extra angles of the quadrilateral $AEFD\;$ $2\epsilon\;$ and $2\phi.\;$
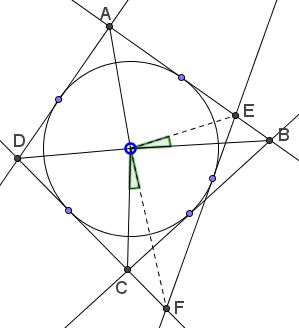
Then $\angle BOC=180^{\circ}-\beta-\gamma$ and $\angle EOF=180^{\circ}-\epsilon-\phi.\;$ But
$2\beta +2\gamma=360^{\circ}-2\alpha -2\delta=2\epsilon+2\phi.$
It follows that $\angle BOC=\angle EOF,\;$ hence, $\angle BOE=\angle COF.\;$ Also $\angle AOE+\angle DOF=180^{\circ}.$
Now, by the Law of Sines, $\displaystyle\frac{AE}{\sin\angle AOE}=\frac{AO}{\sin\angle AEO}\;$ and $\displaystyle\frac{BE}{\sin\angle BOE}=\frac{BO}{\sin\angle BEO}.\;$ Since angles $AEO\;$ and $BEO\;$ are supplementary, we get
$\displaystyle\frac{a}{b}=\frac{AE}{BE}=\frac{AO\cdot\sin\angle AOE}{BO\cdot\sin\angle BOE}.$
Similarly, $\displaystyle\frac{c}{d}=\frac{CF}{DF}=\frac{CO\cdot\sin\angle COF}{DO\cdot\sin\angle DOF}.$ Multiplying the two identities and recollecting that $\angle BOE=\angle COF\;$ and $\angle AOE+\angle DOF=180^{\circ},\;$ we obtain the required $\displaystyle\frac{ac}{bd} = \frac{AO\cdot CO}{BO\cdot DO}.$
Acknowledgment
The problem has been posted by Leo Giugiuc at the CutTheKnotMath facebook page via Miguel Ochoa Sanchez. Proof 1 is by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc. Miguel Ochoa Sanchez referred to Exercices de Géométrie by F.G.-M. This is problem 1218 from the book wherefrom came Proof 2.
What the statement shows is that the ratio $\displaystyle\frac{ac}{bd}\;$ does not depend on the position of the tangent line $\ell\;$ and this is how F.G.-M. formulated his problem. The fact that that ratio equals $\displaystyle\frac{AO\cdot CO}{BO\cdot DO}\;$ came up as a side effect in the proof.
Inscriptible (tangential, circumscribed) Quadrilateral
- When A Quadrilateral Is Inscriptible?
- Inscriptible Quadrilateral: An Illustration
- Inscriptible and Exscriptible Quadrilaterals
- Pairs of Incircles in a Quadrilateral
- Butterfly in Inscriptible Quadrilateral
- Inscriptible Quadrilateral of Triangle Incenters
- Perpendicular Bisectors in an Inscriptible Quadrilateral II
- A Property of Inscriptible Quadrilaterals
- An Inradii Relation in Inscriptible Quadrilateral
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578955
