When a Triangle is A-cute

By definition, a triangle is acute when all three of its angles are less than $90^{\circ}.$ Below are listed several conditions that assure of this property.

Orthocenter

A triangle is acute if and only if its orthocenter is located strictly inside the triangle.

Indeed, the altitudes to a side adjacent to two acute angles passes inside the triangle.

When a Triangle is A-cute, orthocenter

Since this is true for all three altitudes, they may only intersect in the interior of the triangle.

Circumcenter

A triangle is acute if and only if its circumcenter is located strictly inside the triangle.

Indeed, in the circumcircle, a right angle is subtended by a diameter, while an obtuse angle by an arch greater than half the circle. Therefore, in the latter case, the diameter parallel to the chord subtending an obtuse angle never meets the triangle. This is a necessary and sufficient condition for inscribed right and obtuse angles.

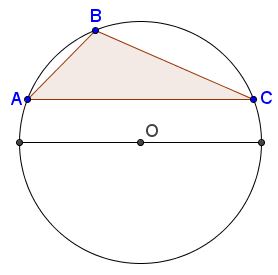
When a Triangle is A-cute, circumcenter

Thus, if all three angles of a triangle are acute, its circumcenter necessarily lies within the triangle.

The Cosine Rule

According to the Law of Cosines, $c^{2}=a^{2}+b^{2}-2ab\cos\gamma,$ where $a,b,c$ are the sides of the triangle and $\gamma$ is the angle opposite side $c.$ $\gamma\lt 90^{\circ}$ is equivalent to $\cos\gamma\gt 0.$ Therefore, we have

A triangle $abc$ is acute if and only if

$a^{2} \lt b^{2} + c^{2},\\ b^{2} \lt a^{2} +c^{2},\\ c^{2} \lt a^{2}+c^{2},$

i.e., when the squares of its sides also form a triangle.

Substitution

The following was communicated to me by Leo Giugiuc.

The previous condition is equivalent to the follwing:

Triangle $abc$ is acute if and only if the are real $x,y,z\gt 0$ such that

$a=\sqrt{y+z},\;b=\sqrt{x+z},\;c=\sqrt{x+y}.$

Indeed, set $x=\displaystyle\frac{-a^{2}+b^{2}+c^{2}}{2},$ $y=\displaystyle\frac{a^{2}-b^{2}+c^{2}}{2},$ $z=\displaystyle\frac{a^{2}+b^{2}-c^{2}}{2}.$ Then, assuming the triangle is acute, e.g., $x+y=c^2,$ etc.

Conversely, if $a,b,c$ are defined through $x,y,z$ as above then, first of all, it can be seen by squaring that, e.g., $a\lt b+c,$ etc. Also, trivially, e.g., $a^{2} \lt b^{2} + c^{2},$ etc., so that the triangle $abc$ is acute.

Extended Pythagorean Theorem

As was established elsewhere, a triangle with angles $\alpha,$ $\beta,$ $\gamma$ is right if and only if

$\cos^{2}\alpha +\cos^{2}\beta +\cos^{2}\gamma =1.$

This follows from a more general formula

$\cos^{2}\alpha +\cos^{2}\beta +\cos^{2}\gamma +2\cos\alpha\cos\beta\cos\gamma=1$

which also implies

Triangle $\alpha\beta\gamma$ is acute if and only if

$\cos^{2}\alpha +\cos^{2}\beta +\cos^{2}\gamma \lt 1.$

In terms of tangents

The following formula holds for the angles of a triangle which is not right

$\tan\alpha + \tan\beta +\tan\gamma = \tan\alpha\tan\beta\tan\gamma.$

From here

Triangle $\alpha\beta\gamma$ is acute if and only if

$\tan\alpha + \tan\beta +\tan\gamma \gt 0.$

Scalar product

If the vertices of a triangle are defined by their coordinates in a Cartesian coordinate system then it is possible to use the scalar (or dot) product to derive the following proposition:

$\Delta ABC$ is acute if and only if

$\overrightarrow{(B-A)}\cdot \overrightarrow{(C-A)}\gt 0,\\ \overrightarrow{(C-B)}\cdot \overrightarrow{(A-B)}\gt 0,\\ \overrightarrow{(A-C)}\cdot \overrightarrow{(B-C)}\gt 0.$

Embedding into tetrahedron

The following was communicated to me by Leo Giugiuc.

A triangle which is a face of an equifacial tetrahedron is necessarily acute.

For a proof see a separate page.

Using angles as side lengths

A triangle is acute iff its angles can be used as the side lengths of another triangle.

For a proof, see a Remark on a separate page.

72354401