Tetrahedron in Parallelepiped
Prism is a $3D$ shape with two equal polygonal bases whose corresponding vertices can be (and are) joined by parallel segments. Parallelepiped is a prism with parallelogram bases. In particular, all six faces of a parallelepiped are parallelograms, with pairs of opposite ones equal.
The eight vertices of a parallelepiped can be grouped into two quadruples each of which contains no adjacent vertices. These could be seen as vertices of a tetrahedron:
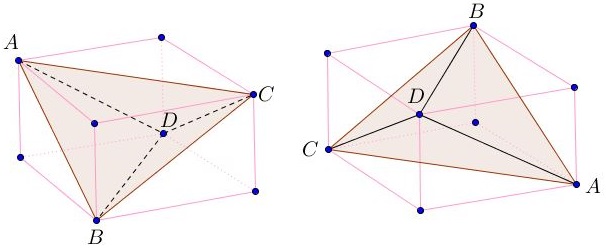
In this manner, every parallelepiped is uniquely associated with a tetrahedron and vice versa because any pair of opposite edges of a tetrahedron uniquely defines two parallel planes, one through each of the edges.
Parallelepiped with all faces rectangular (as in the above diagram) is known as cuboid (a brick is an appropriate but uncommon term.) A parallelepiped whose faces are all rhombi is said to be rhomboid, or rhomboidal.
Tetrahedron is orthogonal or isosceles whenever its opposite edges are orthogonal or, respectively, equal. Tetrahedron with all four faces congruent triangles is called equifacial.
A tetrahedron is orthogonal iff the associated parallelepiped is rhomboidal.
A tetrahedron is isosceles iff the associated parallelepiped is a cuboid.
An isosceles tetrahedron is equifacial.
A tetrahedron is regular iff the associated parallelepiped is a cube.
Proof of #3
By #2, an isosceles tetrahedron is associated with a cuboid - a shape with rectangular faces, i.e., parallelogram faces with equal diagonals. The boundary of every face of the tetrahedron consists of three segments, each being a diagonal of one of the faces of the cuboid, one diagonal from every pair of opposite faces. By the SSS all faces are equal.
The faces of an equifacial tetrahedron are necessarily acute triangles.
Proof of #5
One way to prove that is by employing the Law of Cosines (and the Pythagorean theorem). Let $a,b,c$ denote the lengths of the edges of the associate cuboid. Then the sides of the faces in the tetrahedron equal $\sqrt{a^{2}+b^{2}},$ $\sqrt{b^{2}+c^{2}},$ $\sqrt{a^{2}+c^{2}}.$ By the Law of Cosines,
$(\sqrt{a^{2}+b^{2}})^{2}=(\sqrt{a^{2}+c^{2}})^{2}+(\sqrt{b^{2}+c^{2}})^{2}-2\sqrt{a^{2}+c^{2}}\sqrt{b^{2}+c^{2}}\cos\gamma,$
where $\gamma$ is the angle between the latter two sides. Simplifying we get $c^{2}=\sqrt{a^{2}+c^{2}}\sqrt{b^{2}+c^{2}}\cos\gamma,$ implying that $\cos\gamma\gt 0,$ meaning that $\gamma$ is less than $90^{\circ}.$ Because of the (cyclic) symmetry of the expressions involved, the other two angles are also acute.
Isosceles tetrahedron is associated with cuboid, a parallelepiped with orthogonal faces and edges; this makes it a very special figure (e.g., #3 above). I have collected additional properties of isosceles tetrahedra on separate page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580418
