Small Triangle from Small Triangle
Problem
Solution 1
Let $VXYZ$ be a tetrahedron as depicted below
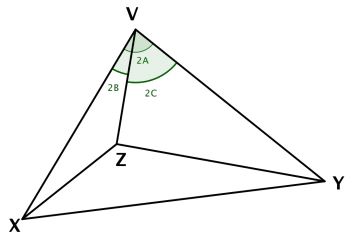
$\angle XVY=2A;\,$ $\angle ZVY=2C;\,$ $\angle XVY=2A.\,$ $VX=VY=VZ=1.$
$\displaystyle \begin{align} XY^2&=VX^2+VY^2-2VX\cdot VY\cdot \cos (\angle XVY)= 1^2+1^2-2\cdot 1\cdot 1\cdot 1\cos 2A\\ &=2(1-\cos 2A)=2(1-1+2\sin^2 A)=4\sin^2 A. \end{align}$
Thus $XY=2\sin A.\,$ Similarly, $XZ=2\sin B,\,$ $YZ=2\sin C.$
In $\Delta XYZ, XY+XZ>YZ\,$ so that $2\sin A+2\sin B\gt 2\sin C,\,$ i.e., $\sin A+\sin B-\sin C\gt 0.\,$ Similarly, $\sin B+\sin C-\sin A\gt 0$ and $\sin C+\sin A-\sin B\gt 0.\,$ Hence,
$\displaystyle \prod_{cycl}(\sin A+\sin B-\sin C)\gt 0.$
Solution 2
WLOG, let $A\geq B\geq C$. $\pi>A+B+C\geq 2A$. Thus, $A$ is acute and so are $B$ and $C$.
From the ordering of ${A,B,C}$ and monotonicity of $\sin$ in the first quarter,
$\sin A \gt \sin B \gt \sin C\,$ and, therefore, $\sin A+\sin B \gt \sin C.$
Additionally,
$\displaystyle \begin{align} \sin A - \sin B\;&= 2\sin\left(\frac{A-B}{2}\right)\cos\left(\frac{A+B}{2}\right) \\ &\lt 2\sin\frac{C}{2}\cos\frac{C}{2}=\sin C. \end{align}$
All the angles in the expressions are acute, $C>A-B$ and $\sin$ increases monotonically in the first quarter, $A+B\gt C$ and $\cos$ decreases monotonically in the first quarter.
$\displaystyle \begin{align} LHS&=(\sin A+\sin B - \sin C)(\sin B + \sin C - \sin A)(\sin C +\sin A -\sin B) \\ &=(\sin A+\sin B - \sin C)[\sin^2 C - (\sin A - \sin B)^2] \\ &> 0, \end{align}$
from the two inequalities already proven.
Solution 3
The numbers $A, B,\pi-A-B\,$ are angles of a triangle. Hence, the triangle inqualities, combined with the Law of Sines, give $\sin A+\sin B\gt \sin(\pi-A-B)=\sin(A+B).$
Suffice it to show that $\sin (A+B)\ge\sin C\,$ which is equivalent to $\displaystyle \sin\left(\frac{A+B-C}{2}\right)\cos\left(\frac{A+B+C}{2}\right)\ge 0,$ which is true sine $\displaystyle 0\lt\frac{A+B-C}{2}\lt\frac{\pi}{2}\,$ and also $\displaystyle 0\lt\frac{A+B+C}{2}\lt\frac{\pi}{2}.$
Done.
Remark
The three triangle inequalities in the problem inform us that the quantities $A,B,C\,$ may be looked at as the side lengths of a triangle. The condition $A+B+C\lt\pi\,$ tells us that the triangle is not big.
The conclusion of the problem is equivalent to saying that $\sin A,\,$ $\sin B,\,$ and $\sin C\,$ also form a triangle, whose perimeter does not exceed $3,\,$ hence the caption.
Furthermore, the given triangle is necessarily acute: $0\lt A,B,C\displaystyle \lt\frac{\pi}{2}.\,$ This is so because, say, $\displaystyle A\gt\frac{\pi}{2}\,$ would lead to $\displaystyle B+C\lt\frac{\pi}{2},\,$ in contradiction with $A\lt B+C.$
We may also claim that the inverse is also true: the angles of an acute triangle satisfy the three triangle inequalities. Indeed, from $A+B+C=\pi\,$ and, say, $A\lt\displaystyle \frac{\pi}{2},\,$ it follows that $B+C\gt\displaystyle \frac{\pi}{2}\gt A.$
Thus, a triangle is acute iff its angles can be used as the side lengths of a triangle.
Acknowledgment
Dan Sitaru has kindly sent me this problem along with the above solution of his. Solution 2 is by Amit Itagi; Solution 3 is by Leo Giuguc.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73584738
