Two Cevians and Proportions in a Triangle, II

Here is a problem #37 from the 1965 Annual High School Contest

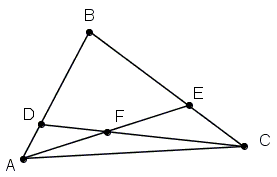
Point D is selected on side AB of triangle ABC in such a way that AD:BD = 1:3 and point E is selected on side BC so that CE:BE = 1:2. The point of intersection of AE and CD is F. Then

DF/CF + AF/EF is

(A) 4/5  (B) 5/4  (C) 3/2  (D) 2  (E) 5/2

Solution

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Point D is selected on side AB of triangle ABC in such a way that AD:BD = 1:3 and point E is selected on side BC so that CE:BE = 1:2. The point of intersection of AE and CD is F. Then

DF/CF + AF/EF is

(A) 4/5  (B) 5/4  (C) 3/2  (D) 2  (E) 5/2

1965 American High School Contest, Problem 37

Solution

Draw the third cevian BK:

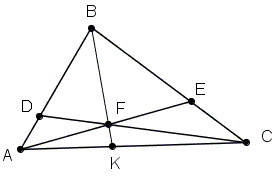
1965 American High School Contest, Problem 37, Solution 2

Then, by Ceva's theorem

AD/BD · BE/CE · CK/AK = 1

so that

1/3 · 2/1 · CK/AK = 1

from which CK/AK = 3/2.

By van Obel's theorem,

CF/DF = CE/BE + CK/AK = 1/2 + 3/2 = 2 and
AF/EF = AK/CK + AD/BD = 2/3 + 1/3 = 1.

It follows that DF/CF + AF/EF = 1/2 + 1 = 3/2.

(Another solution is available eslewhere.)

References

  1. C. T. Salkind, The Contest Problem Book II, MAA, 1996

Menelaus and Ceva

72205230