Altitudes and the Power of a Point
What Is This About?
A Mathematical Droodle
Explanation
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
The applet provides an illustration to a problem from an outstanding collection by T. Andreescu and R. Gelca:
Let ABCD be a convex quadrilateral inscribed into a semicircle s of diameter AB. The lines AC and BD intersect at E and the lines AD and BC at F. The line EF intersects semicircle s at G and the line AB at H. Prove that E is the midpoint of the line segment GH if and only if G is the midpoint of the line segment FH.
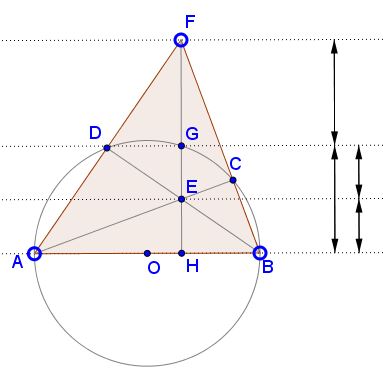
The statement follows from a more general fact that GH is the geometric mean of EH and FH:
which, for example, also implies that if E divides GH in the golden ratio then the same is true of G with respect to FH. So, let's prove (1).
The right triangles AFH and ABD share an angle at A and are thus similar. Similarly, the right triangles ABD and EBH that share an angle at B are also similar. By transitivity, triangles AFH and EBH are similar. The latter similarity implies the proportion:
AH/EH = FH/BH
which is to say
But ABG is a right triangle with hypotenuse GH so that AH·BH = GH2 which together with (2) implies (1).
Note that AH·BH is the power of point H with respect to the given circle.
References
- T. Andreescu, R. Gelca, Mathematical Olympiad Challenges, Birkhäuser, 2004, 5th printing, 1.3.9 (p. 12)
Power of a Point wrt a Circle
- Power of a Point Theorem
- A Neglected Pythagorean-Like Formula
- Collinearity with the Orthocenter
- Circles On Cevians
- Collinearity via Concyclicity
- Altitudes and the Power of a Point
- Three Points Casey's Theorem
- Terquem's Theorem
- Intersecting Chords Theorem
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
| 
