Intersecting Chords Theorem - Hubert Shutrick's PWW
Given a point \(P\) in the interior of a circle, pass two lines through \(P\) that intersect the circle in points \(A\) and \(D\) and, respectively, \(B\) and \(C\). Then \(AP\cdot DP = BP\cdot CP\).
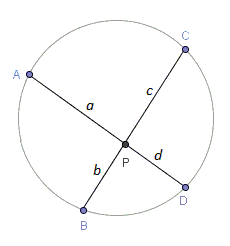
If \(a=AP\), \(b=BP\), \(c=CP\), and \(d=DP\), then the Intersecting Chors Theorem is expressed as
\(a\cdot d = b\cdot c\).
(The applet below illustrates a proof by Hubert Shutrick. Points \(A\), \(B\), \(C\), \(D\), \(O\), \(R\) are draggable. Point \(O\) is the center of the given circle, \(R\) - a point on the circle.)
Created with GeoGebra
Proof
This proof without words is due to Hubert Shutrick.
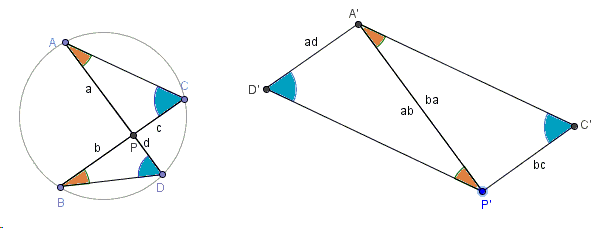
(For an explanation - if needed, see a slightly modified version.)
This is a simple example showing how the product identities that you get algebraically from similar triangles can be illustrated. A more sophisticated example is the proof of Ptolemy's theorem with the Pythagorean theorem as the special case when the quadrilateral is a rectangle.
Power of a Point wrt a Circle
- Power of a Point Theorem
- A Neglected Pythagorean-Like Formula
- Collinearity with the Orthocenter
- Circles On Cevians
- Collinearity via Concyclicity
- Altitudes and the Power of a Point
- Three Points Casey's Theorem
- Terquem's Theorem
- Intersecting Chords Theorem
- Intersecting Chords Theorem - a Visual Proof
- Intersecting Chords Theorem - Hubert Shutrick's PWW
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73564728
