Intersecting Chords Theorem - a Visual Proof

Given a point \(P\) in the interior of a circle, pass two lines through \(P\) that intersect the circle in points \(A\) and \(D\) and, respectively, \(B\) and \(C\). Then \(AP\cdot DP = BP\cdot CP\).

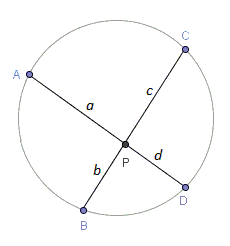
Intersecting Chords Theorem - statement

If \(a=AP\), \(b=BP\), \(c=CP\), and \(d=DP\), then the Intersecting Chors Theorem is expressed as

\(a\cdot d = b\cdot c\).

(The applet below illustrates the proof. Points \(A\), \(B\), \(C\), \(D\), \(O\), \(R\) are draggable. Point \(O\) is the center of the given circle, \(R\) - a point on the circle.)

Proof

This proof is a slightly modified version of the one suggested by Hubert Shutrick.

Apply homothety with center \(P\) and the coefficient \(b\) to \(\Delta APC\) and another with the coefficient \(a\) to \(\Delta BPD\).

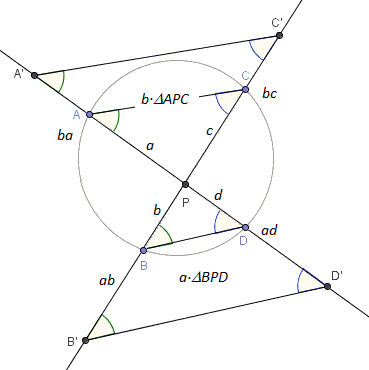
Intersecting Chords Theorem - proof

Observe that, as two inscribed angles subtended by the same arc, \(\angle CAD =\angle CBD\), and, similarly, \(\angle ACB =\angle ADB\). Since homotheties preserves angles, we also have \(\angle C'A'D' =\angle C'B'D'\) and \(\angle A'C'B' =\angle A'D'B'\). By the construction, \(A'P = ba = ab = B'P\), making triangles \(A'PC'\) and \(B'PD'\) equal, so that \(C'P=D'P\) but \(C'P=bc\) whereas \(D'P=ad\). Therefore, \(bc=ad\).


Power of a Point wrt a Circle

  1. Power of a Point Theorem
  2. A Neglected Pythagorean-Like Formula
  3. Collinearity with the Orthocenter
  4. Circles On Cevians
  5. Collinearity via Concyclicity
  6. Altitudes and the Power of a Point
  7. Three Points Casey's Theorem
  8. Terquem's Theorem
  9. Intersecting Chords Theorem
  10. Intersecting Chords Theorem - a Visual Proof
  11. Intersecting Chords Theorem - Hubert Shutrick's PWW

|Contact| |Front page| |Content| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72504053