First Geometric Interpretation of Negative and Complex Numbers
John Wallis (1616-1703), a contemporary of I. Newton, was the first to divest the notion of number from its traditional association with quantity. As quantities neither negative or complex numbers make a lot of sense. The problem was not in denying their existence but in finding a suitable model: Fiction is a form in search of an interpretation [Dantzig, p. 205, Swetz, p. 481]. As Wallis wrote in Algebra (1673) [Smith, pp. 46-54],
| |
... But it is also Impossible, that any Quantity (though not a Supposed Square) can be Negative. Since that is not possible that any Magnitude can be Less than Nothing, or any Number Fewer than None.
Yet is not that Supposition (of Negative Quantities) either Unuseful or Absurd; when rightly understood. And though, as to the bare Algebraick Notations, it import a Quantity less than nothing: Yet, when it comes to a Physical Application, it denotes as Real a Quantity as if the Sign were +; but to be interpreted in a contrary sense.
|
Subsequently, Wallis interprets negative numbers as distances in the direction opposite to the positive, to the left of a given point. His geometric interpretation of complex numbers begins with the following diagram:
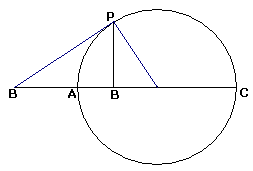
where the circle has AC as a diameter and A plays the role of the origin. (Wallis still does not use the second, vertical axis.) He explains:
| |
If (for instance) Forward from A, I take AB = +b; and Forward from thence, BC = +c; (making AC = +AB+BC = +b+c, the Diameter of a Circle:) Then is the Sine, or Mean Proportional BP =  +bc.
But if Backward from A, I take AB = -b; and then Forward from that B, BC = +c; (making AC = -AB+BC = -b+c, the Diameter of the Circle;) Then is the Tangent or Mean Proportional BP = -bc.
|
He then proceeds immediately to apply the new interpretation of complex numbers to illustrate the SSA construction of a triangle: Given the elements AP, BP and  PAB, find the base AB.
Applying the Pythagorean theorem to DBPC we find that
| (1) |
AB = AC ± (PB2 - PC2).
|
This is of course provided that PB ≥ PC. Ingeniously, Wallis applies the same formula (1) even when PB < PC. How? For the "real" case PB ≥ PC, find a circle for which BC serves as the "Sine" in Wallis' previous derivation. It could be, say, the circle centered at P with radius PB. From here, think of how the diagram could be adapted to make BC tangent to the circle. To this end it is convenient to consider a circle with PC as a diameter. (Both cases are illustrated by the applet below. One can move points A and P and an unmarked point that determines the radius PB of the orange circle centered at P.)
For the "complex" case, Wallis reformulates the problem as the question of finding points B that satisfy (1). Instead of constructing DABP with the given data, he does manage to specify two points, now in the plain, that are uniquely determined by the given data:
| |
This Impossibility in Algebra, argues an Impossibility of the case proposed in Geometry; and that the Point B cannot be had, (as was proposed,) in the Line AC, however produced (forward or backward) from A.
Yet are there Two Points designed (out of that Line, but) in the same Plain; to either of which, if we draw the lines AB, BP we have a triangle; whose sides AP, BP are such as were required: and the angle PAC, and the altitude PC, (above AC, though not above AB,) such as was proposed; And the Difference of Squares of PB, PC, is that of CB.
|
To accomplish this feat, Wallis defines B at the intersection of the circle centered at P with radius PB and the circle having PC as a diameter. In DBCP so defined the right angle occurs at the vertex B instead of C.
| |
|
Now, if we set x = AB, AC = PB = b/2, and PC = a, and interpret the algebraic operations as addition and subtraction of vectors, then Wallis' method in both the "real" and "complex" cases reduces to the solution of the quadratic equation x2 - bx + a = 0:
| |
x = b/2 ± (b2/4 - a).
|
References
- T. Dantzig, NUMBER: The Language of Science, The Free Press, 1954
- D. E. Smith, A Source Book in Mathematics, Dover, 1959
- F. J. Swetz, From Five Fingers To Infinity, Open Court, 1996 (3rd printing)
Complex Numbers
- Algebraic Structure of Complex Numbers
- Division of Complex Numbers
- Useful Identities Among Complex Numbers
- Useful Inequalities Among Complex Numbers
- Trigonometric Form of Complex Numbers
- Real and Complex Products of Complex Numbers
- Complex Numbers and Geometry
- Remarks on the History of Complex Numbers
- First Geometric Interpretation of Negative and Complex Numbers
- Complex Numbers: A Dynamic Tool
- Cartesian Coordinate System
- Fundamental Theorem of Algebra
- Complex Number To a Complex Power May Be Real
- One Can't Compare Two Complex Numbers
- Problems
Copyright © 1996-2008 Alexander Bogomolny
|
