Geometric Mean In Trapezoid
The following engaging fact was brought to my attention by Miguel Ochoa Sanchez from Peru:
Given a trapezoid $ABCD,\;$ $AB\parallel CD.\;$ The diagonals of the trapezoid cut the figure into four triangles, with the areas as shown below:
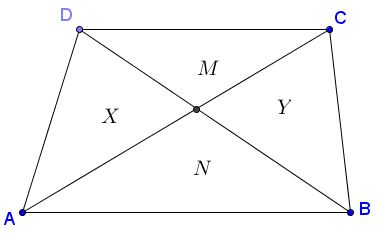
Then $X\cdot Y=M\cdot N.$ and, since $X=Y,\;$ also $X=\sqrt{M\cdot N}.$
Proof
Denote the pieces of the diagonals $a,b,c,d,\;$ as shown in the diagram below. Let $\alpha\;$ be the angles between the diagonals:
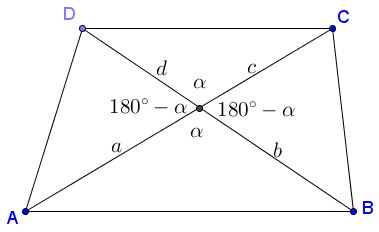
Then
$\begin{align} X&=\frac{1}{2}ad\sin\alpha,\\ N&=\frac{1}{2}ba\sin\alpha,\\ Y&=\frac{1}{2}cb\sin\alpha,\\ M&=\frac{1}{2}dc\sin\alpha,\\ \end{align}$
Now $X\cdot Y=\frac{1}{4}abcd\cdot\sin^2\alpha=M\cdot N.$
There is more to that. By Euclid I.37, $X+M=[\Delta ACD]=[\Delta BCD]=Y+M\;$ so that $X=Y\;$ and, finally $X=\sqrt{M\cdot N}.\;$
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73603628
