A Lemma of Equal Areas

Bui Quang Tuan came up with a simple but surprisingly useful lemma:

Let A, B, C be three collinear points. D, E are two points on one side with respect to line that contains A, B, C and such that AD||BE and BD||CE. F is midpoint of AC. Then Area(DEF) = (Area(ABD) + Area(BCE))/2.

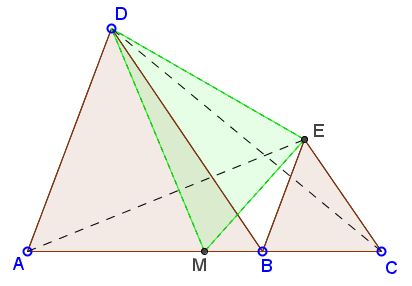
Observe that if F coincides with B, the claim is rather obvious, for then the three triangles DEF, ABD, and BCE are equal. Interestingly, the equality of the areas holds in a more general case.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

Proof

Buy this applet
What if applet does not run?

Proof

In the trapezoid ABED, Area(ABD) = Area(AED) because the two triangles share a base AD and are in the same parallel lines, meaning that the altitudes to AD from B and E are equal. Similarly, in the trapezoid BCED, Area(BCE) = Area(CDE). Adding the two identities,

Area(ABD) + Area(BCE) = Area(AED) + Area(CDE).

Let h_a, h_f, h_c be the lengths of the perpendiculars to DE from A, F, and C, respectively. h_f = (h_a + h_c)/2. On the other hand, Area(AED) = DE·h_a/2 and Area(CDE) = DE·h_c/2. Therefore,

	Area(ABD) + Area(BCE)	= Area(AED) + Area(CDE)
		= DE·(h_a + h_c)/2
		= DE·h_f
		= 2·Area(DEF).

Note

If h_b is the altitude from B to DE, then - using similarities - h_b/h_a = h_c/h_b, from which Area(ADE)×Area(CDE) = Area(BDE)². As a consequence of the above, we also have Area(ABD)×Area(BCE) = Area(BDE)².

40620593