Artisans vs Mathematicians

Mathematicians made it their business to solve problems (and communicate the problems and their solutions to other mathematicians.) New problems may be suggested by internal advancement of mathematics or be brought from outside by practitioners of other disciplines. Solutions may be good or bad depending on how well they answer the question that prompted their development. This is just common logic that applies to any purposeful endeavor. Solutions are assumed to solve the problems they were developed to solve. Naturally, a problem may have many solutions whose nature may be related not only to the problem itself but to the tastes and skills of the problem solver. Fascinating and edifying examples are found in the 10^th century treatise On Those Parts of Geometry Needed by Craftsman by the famous Persian mathematician Abul Wafa al-Buzjani. (All the quotes below come from a Mathematics Horizon article by R. Sarhangi and S. Jablan.)

Buzjani wrote that he participated in meetings between artisans and mathematicians:

At some sessions, mathematicians gave instructions on certain principles and practices of geometry. At others, they worked on geometric constructions of two- and three-dimensional ornamental patterns or gave advice on the applications of geometry to architectural construction.

In a chapter titled On Dividing and Assembling Squares, Buzjani describes different attitudes towards geometry exhibited by artisans and mathematicians:

A number of geometers and artisans made errors in the matter of these squares and their assembling. The geometers made errors because they don't have practice in applied constructing, and the artisans because they lacked knowledge of reasoning and proof.

And further

I was present at a meeting in which a number of geometers and artisans participated. They were asked about the construction of a square from three (equal) squares. Geometers easily constructed a line such that the square of it is equal to the three squares but none of the artisans was satisfied. They wanted to divide those squares into pieces from which one square can be assembled.

It appears that the artisans perceived the problem as that of dissection, whereas the mathematicians' interpretation was entirely different. The mathematicians thought that the question was to construct a square whose area is three times the area of a given square (something along the line of duplication of the cube.)

So from the mathematicians point of view the answer was pretty simple based on the Pythagorean theorem:

Starting with an isosceles right triangle with hypotenuse √2 form successively right triangles with hypenuse √3, √4, and so on.

The artisans were not satisfied with this approach. In their view, the question was of practical nature: given three equal square tiles, how to cut them into pieces that may be reassembled into a bigger square? Many solutions were presented, some correct, other not, although at first glance they looked ok. One of the latter kind is presented in the diagram below:

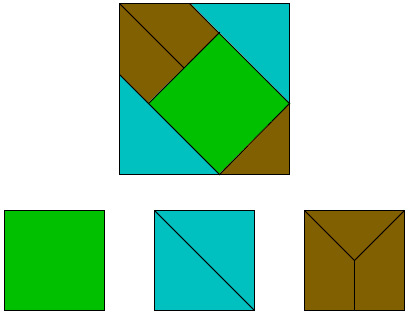
To which Buzjani supplied a comment:

Some of the artisans locate one of these squares in the middle and divide the next one on its diagonal and divide the third square into one isosceles right triangle and two congruent trapezoids and assemble together as it is seen in the figure.

For a lay person not familiar with the science of geometry, this solution seems correct. However, it can be shown that this is not the case. It is true that the resulting shape has four right angles. It is also true that each side of the larger shape seems to be one unit plus one half of the diagonal of the unit square. However, this construction does not result in a square because the diagonal of the unit square (which is the hypotenuse of the assembled larger triangle) is an irrational number but the measure of the line segment that this hypotenuse is located on in the larger shape is one and a half units, which is a rational number.

After so berating the artisans' approach, Buzjani offers a solution acceptable to the artisans while being mathematically correct:

But on the division of the squares based on reasoning we divide two squares along their diagonals. We locate each of these four triangles on one side of the third square in such a way that one vertex of the acute angle of the triangle is located on a vertex of the square. Then by means of line segments we join the vertices of the right angles of four triangles. From each larger triangle a smaller triangle will be cut using these line segments. We put each of these triangles in the congruent empty space next to it to complete the square.

The diagram below illustrates Buzjani's solution (see also, [Frederickson, p. 32]):

Obviously, this particular construction can be interpreted as reassembling a square of the pieces cut off two squares of which one has the area twice that of the other. The construction immediately extends to combining two arbitrary squares into one.

It is hard to imagine that Buzjani has not observed such an extension, especially because he was interested in the problem of combining two squares of arbitrary dimensions. The construction as such has been published a millennia later in Mathematics Magazine by Poo-sung Park and included into the Proofs Without Words II collection. Buzjani himself came up with another approach that required fewer cuts and pieces. Along the way he also proved the Pythagorean theorem:

Buzjani's "rational/irrational" argument is elegant but is rather on the side of the "pure mathematics" construction of √3. If you actually try following the artisans' suggestion the result will look like

Indeed, the side of the alleged square should be, say, x = 1 + √2/2, so that its diagonal would be x√2 = 1 + √2 ≈ 2.4142... whereas the pieces put together along the diagonal of the combined shape stretch to the length of 2.5. The error is in the order of 3.4% and is quite noticeable.

On the other hand, the artisans may have been concerned only with a practical (read approximate) solution. Half a millennia later, A. Dürer, a notable amateur mathematican himself, in a treatise intended for the use by craftsmen, gave two constructions of regular pentagon without so much as a mention that one of them was approximate (with an angular error around 1%.)

... to be continued ...

References

G. N. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997
R. B. Nelsen, Proofs Without Words II, MAA, 2000
R. Sarhangi, S. Jablan, Elementary Constructions of Persian Mosaics, Math Horizons, Sept. 2006, 10-13

MANIFESTO

71542607