Four Problems Of Antiquity
Three geometric questions raised by the early Greek mathematicians attained the status of classical problems in Mathematics. These are:
- Doubling of the cube
Construct a cube whose volume is double that of a given one. - Angle trisection
Trisect an arbitrary angle. - Squaring a circle
Construct a square whose area equals that of a given circle.
Often another problem is attached to the list:
The problems are legendary not because they did not have solutions, or the solutions they had were unusually hard. No, numerous simple solutions have been found yet by Greek mathematicians. The problem was in that all known solutions violated an important condition for this kind of problems, one condition imposed by the Greek mathematicians themselves:
Valid solutions to the construction problems are assumed to consist of a finite number of steps of two kinds only: drawing a straight line through two points with a ruler (or rather a straightedge as no marks are allowed on the ruler) and drawing a circle with a given center and radius.
You are referred to solutions of problems #2 and #3 as examples of existent solutions. That no solution exists subject to the self-imposed constraints has been proved only in the 19th century.
![]()
Doubling the Cube
Doubling the Cube, the most famous of the collection, is often referred to as the Delian problem due to a legend that the Delians had consulted Plato on the subject. In another form, the story asserts that the Athenians in 430 B.C. consulted the oracle at Delos in the hope to stop the plague ravaging their country. They were advised by Apollo to double his altar that had the form of a cube. As a result of several failed attempts to satisfy the god, the pestilence only worsened and at the end they turned to Plato for advice. (According to Rouse Ball and Coxeter, p 340, an Arab variant insists that the plague had broken between the children of Israel but the name of Apollo had been tactfully omitted.) According to a letter from the mathematician Eratosthenes to King Ptolemy of Egypt, Euripides mentioned the Delian problem in one of his (now lost) tragedies.
Angle trisection
That there may be a difficulty trisecting an angle is rather surprising. In the classical framework, one draws two kinds of lines: straight lines and circles. The same easy approach applies to bisecting both straight line segments and circular arcs:
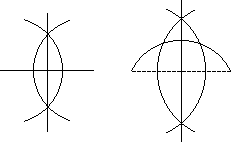
The problem of trisecting a line segment is no more difficult than finding its n-th part for an arbitrary n. However, the general problem of trisecting and angle (i.e., trisecting an arbitrary angle) is not solvable in a finite number of steps. Two points must be made.
Firstly, some angles are trisectable with ruler and compass. An obvious example is supplied by the three quarters of the straight angle - 67.5o. (The angle itself is constructible as it is obtained by two consecutive angle bisections. Its third is obtained along the way.) Angles of 30o (draw a right triangle with a side 1 and hypotenuse 2) and 45o (bisect the right angle) are both constructible. Therefore, the latter also admits a classical trisection. However, and this is where the difficulty lies, an arbitrary angle can't be trisected with a ruler and a compass, as stated above.
Secondly, consider the geometric series 1/4 + 1/16 + 1/64 + ... that adds up to 1/3. Once we know how to bisect an angle, we may also find its 2-n-th part, for any n. In particular, one may construct 1/4, 1/16, ... of any angle and, in principle, find its third after an infinite number of steps. This solution is universal but requires a forbidden (infinite) number of steps.
The problem had been settled in 1837 by Pierre Laurent Wantzel (1814-1848) who had proved that there was no way to trisect a 60o angle in the classical framework.
Constructing a regular heptagon
3-, 4-, 5-, and 6-gons (i.e., regular triangles, squares, pentagons, and hexagons) are all and easily constructible. Octagons are constructible on the heels of squares with a single angle bisection. All polygons obtained from the above four by doubling the number of sides are also constructible. Not so a heptagon, a 7-sided polygon.
In 1796, at the age of 19, Gauss have shown that a regular heptadecagon (a 17-sided polygon) is constructible. As Gauss showed, the heptadecagon was only a particular case of a family of constructible regular polygons. Any N-gon, where N is in the form 2np1...pm, where pi's are distinct Fermat primes (i.e. primes in the form 22k + 1), is constructible. Wantzel later proved that no other regular polygon has this property.
Squaring a circle
Surprisingly, the impossibility proofs for the three cited problems: doubling the cube, trisecting an angle, and constructing a regular heptagon, all fall into the same framework. Each depends on showing that roots of certain third degree polynomial equations are not constructible.
The problem of squaring of a circle found itself in a completely different category. It has been solved later in the 19th century when the number π has been shown to be transcendental. Not being algebraic, it is automatically not constructible. However, the area of a circle with radius 1 is exactly π. If a square with such area were constructible, so would be the number itself.
References
- W.W.Rouse Ball and H.S.M.Coxeter, Mathematical Recreations and Essays, Dover, 1987
- W.W.Rouse Ball, A Short Account of the History of Mathematics, Dover, 1960
- J.H.Conway and R.K.Guy, The Book of Numbers, Springer-Verlag, NY, 1996.
- R. Courant and H.Robbins, What is Mathematics?, Oxford University Press, NY, 1996.
- H.Dorrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY,1965
- W.Dunham, The Mathematical Universe, John Wiley & Sons, NY, 1994.
- The History of Mathematics, ed J.Fauvel and J.Gray, The Open University, 1987
- M.Kac and S.M.Ulam, Mathematics and Logic, Dover Publications, NY, 1992
- O.Ore Number Theory and Its History, Dover, 1988
- I.Stewart, Concepts of Modern Mathematics, Dover, 1995
Constructible Numbers, Geometric Construction, Gauss' and Galois' Theories
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580036
