Approximate Construction of Regular Pentagon by A. Dürer

Albrecht Dürer (1471-1528), a pioneer German painter, engraver and a famous amateur mathematician, was known to be interested, among many other things, in pentagonal plane tessellations, pentagonal ornaments and practical construction of regular polygons, pentagons in particular. In his 1525 book, Underweysung der Messing mit Zirkel und Richtscheit (Treatise on Mensuration with Compass and Ruler), intended for architects and draftsmen he gave an approximate construction of a regular pentagon. The construction uses straightedge and comas whose opening is set only once and remains fixed in the course of the construction.

1. Start with a segment AB and draw two circles A(B) and B(A), one with center A and passing through B, the other with center B and passing through A. Mark the intersection points N and Q of the two circles.

2. With the center Q and the same radius draw circle Q(A) passing through A and B. Mark point P where it crosses line NQ.

3. Let E be the intersection of PS with A(B) and C the intersection of PR with B(A).

4. Mark D the intersection of E(A) and C(B), as shown.

ABCDE is an almost regular pentagon. Let's see that this is indeed so.

Concentrate on the circle centered at Q, (Q). By construction,

as if we were trying to inscribe a regular hexagon into (Q). It follows that

1. RS is a diameter of (Q),
2. RAS = RBS = 90°,
3. BRS = 30°,
4. BR = √3/2·RS = √3 (since RS = 2),
5. ARB = 30°,
6. ARP = BRP = 15°.

Apply the Law of Sines to ΔBCR:

sin(BRC) / BC = sin(BCR) / BR,

wherefrom

sin(BCR) = √3·sin(15°),

which gives BCR ≈ 26.6338798...°. CBR then is approximately 138.36612...° and, since ABR = 30°, ABC ≈ 108.36612..°, very close to 108° - the internal angle of the regular pentagon. Of course angles ABC and BAE are equal.

We can further determine the remaining angles of ABCDE: angles at C and E are a little less than 108° while the angle at D is a little more than 109° - still not too bad.

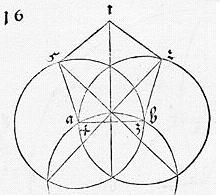
It is a curious observation that Dürer has not mentioned the fact that the construction is merely approximate listing it along with an exact one.

References

1. R. A. Simon, Approximate Construction of Regular Polygons: Two Renaissance Artists, Convergence, MAA
2. D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, 1991

• Approximate Construction of Regular Pentagon by A. Durer
• Construction of Regular Pentagon by H. W. Richmond
• Inscribing a regular pentagon in a circle – and proving it
• Regular Pentagon Construction by Y. Hirano