How Fast Does One's Shadow Grow?
It's a common perception that when a fellow strolls at night away from a street lamp, his or her shadow grows with an increasing speed. Have you ever tried to verify whether that is indeed so or not? John Adams does this in his wonderful book X and the City.
The diagram below illustrates the situation. Assume \(L\) is the height of the electric pole, \(h\) is your height, \(x = x(t)\) is your distance from the base of the pole, and \(w = w(t)\) is the length of your shadow due to the light at the top of the pole; \(t\) is time. \(L\) and \(h\) are constant.
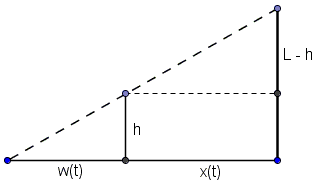
The diagram shows two pairs (vertical and horizontal) of parallel lines that lead to a proportion:
\(\displaystyle \frac{x(t)}{L-h} = \frac{w(t)}{h}\).
In other words,
\(w(t) = Cx(t)\),
where \(\displaystyle C=\frac{h}{L-h}\), a constant. The equation shows that, provided your speed is constant, the shadow lengthens at a constant rate; the common perception is misleading.
David Singmaster in a more recent book observes that the rate $C,$ relative to your position, may in fact be less than $1.$ In other words, the rate of your shadow growth may be slower than you are. Let, for example, $L=15''$ and $h=6''.$ Then $C=\displaystyle\frac{6}{9}=\frac{2}{3}.$ On the other hand, the rate of the shadow relative to the base of the pole, i.e., $\displaystyle\frac{w(t)+x(t)}{x(t)}=C+1=\frac{L}{L-h}$ is always greater than $1.$ Thus, the shadow's head always moves faster than you do (but still at a constant speed), while the shadow's length may grow slower than you move (but still at a constant rate).
References
- J. A. Adam, X and the City: Modeling Aspects of Urban Life, Princeton University Press, 2012
- D. Singmaster, Problems for Metagrobologists, World Scientific, 2016, #139
MANIFESTO
- Manifesto. Interactive Mathematics Miscellany and Puzzles
- Is anything wrong with math education?
- Can I do anything?
- Math was the most difficult subject I ever...
- Is Mathematics all around us?
- How Fast Does One's Shadow Grow?
- Is math beautiful?
- Do we need Mathematics?
- Proofs in Mathematics
- Artisans vs Mathematicians
- Pleasant math morsels
- Mathematics and Puzzles
- Learn Mathematics for Its Value
- Need Mathematics Taught in School Be Relevant?
|Contact| |Front page| |Contents| |Manifesto|
Copyright © 1996-2018 Alexander Bogomolny73574485
