Three Travelers in Uniform Motion
Problem

Solution 1
We shall express the condition that points $P,Q,R\,$ are collinear as $R\in (PQ),\,$ provided $P\ne Q.$
Let's use a system of coordinates with one of the travelers at the origin. Then the problem reduces to the following:
For a given point $A,\,$ prove that, if points $P\,$ and $Q\,$ move uniformly along straight lines, then the event $A\in (PQ)\,$ may occur not more than twice, provided at time $t=0\,$ $A\notin (PQ).$
Assume that, for some $t=t_1,\,$ the travelers $P\,$ and $Q\,$ have been located at points $B\,$ and $C\,$ such that $A\in (BC).\,$
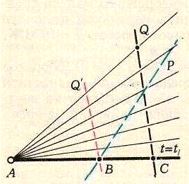
Introduce an imaginary traveler $Q'\,$ that moves along the road parallel to that of $Q,\,$ who was at $B\,$ at the moment $t_1\,$ and such that at all times $A\in (QQ').$
Clearly, the conditions $A\in (PQ),\,$ $A\in (PQ'),\,$ and $Q'\in (AP)\,$ are equivalent (if, of course $P\ne Q').$
Obviously $Q'\,$ moves with a constant speed. Therefore the line $PQ'\,$ remains parallel to itself so that, at best, it may pass through $A\,$ at only one moment, say $t_2\ne t_1.$ (Note that, due to the premises of the problem, $P\,$ and $Q'\,$ can't coincide or move along $AB\,$ all the time.)
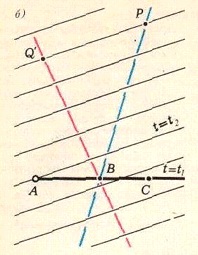
It's not hard to give examples where the travelers are never collinear, or are collinear just once or twice. Without a proof, let's observe that, if two points $P\,$ and $Q\,$ move uniformly along two straight lines, then the lines $PQ\,$ are 1) either all concurrent, or 2) are all parallel, or 3) are all tangent to a unique parabola, the envelope of the set of those lines:
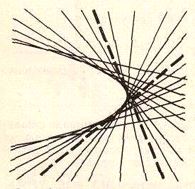
This makes it obvious that through any point in the plane pass no more than two lines $PQ.$
Solution 2
Let's introduce coordinates $Oxy.\,$ The condition that two vectors $\vec{v}=(v_x,v_y)\,$ and $\vec{w}=(w_x,w_y)\,$ are collinear may be expressed as $v_xw_y=v_yw_x.\,$ We shall use the following notation: $[\vec{v},\vec{w}]=v_xw_y-v_yw_x.\,$ The function $(\vec{v},\vec{w})\,\mapsto\,[\vec{v},\vec{w}]\,$ has the following properties:
$[\lambda\vec{v},\vec{w}]=[\vec{v},\lambda\vec{w}]=\lambda [\vec{v},\vec{w}],\\ [\vec{v}+\vec{w},\vec{u}]=[\vec{v},\vec{u}]+[\vec{w},\vec{u}],\\ [\vec{u},\vec{v}+\vec{w}]=[\vec{u},\vec{v}]+[\vec{u},\vec{w}],$
for and vectors $\vec{u},\vec{v},\vec{w}\,$ and a real number $\lambda.\,$ To remind, $[\vec{v},\vec{w}]=0\,$ iff the two vectors are collinear. (The quantity $[\vec{v},\vec{w}]\,$ has a simple geometric meaning: this is the area of the parallelogram formed by the two vectors.)
Now, let points $P,Q,R\,$ move uniformly along straight lines. Then
$\vec{RP}=\vec{a}+t\vec{v},\,\vec{RQ}=\vec{b}+t\vec{w},$
where $t\,$ is time, and $\vec{a},\vec{b},\vec{v},\vec{w}\,$ are vectors independent of $t.\,$ Formulas (1) follow from the fact that if point $M\,$ moves with velocity $\vec{u},\,$ then $\vec{OM}=\vec{OM_0}+t\vec{u},\,$ where $M_0\,$ is the location of $M\,$ at $t=0,\,$ while $O\,$ is a fixed point in the plane.
The condition $R\in (PQ)\,$ can be expressed as
(1)
$[\vec{v},\vec{w}]t^2+([\vec{a},\vec{w}]+[\vec{b},\vec{v}])t+[\vec{a},\vec{b}]=0,$
which is a quadratic equation in $t.\,$ Though some of its coefficients may vanish, but, according to the conditions of the problem, (1) does not hold at some moment in time, so that (1) is not trivial. It follows that $R\in (PQ)\,$ may occur not more than for two time moments $t.$
Solution 3
Let the position of the first two travelers relative to the third one be $\vec{a}+t\vec{u}\,$ and $\vec{b}+t\vec{v}\,$ where $t\,$ is time. For these to be collinear, $(\vec{a}+t\vec{u})\times (\vec{b}+t\vec{v})=\vec{0}\,$ or $(\vec{a}\times \vec{b})\cdot [(\vec{a}+t\vec{u})\times (\vec{b}+t\vec{v})]=0\,$ which is a quadratic equation in $t,\,$ and allows for a maximum of two real $t's.$
Solution 4
Let $M_i:\,\mapsto x_i+tv_i,\,$ $i=1,2,3\,$ be the positions of the three travelers. Let $P:\,\mapsto \det(\overrightarrow{M_1(t)M_2(t)},\overrightarrow{M_1(t)M_3(t)}).\,$ The travelers are collinear at time $t\,$ iff $P(t)=0.\,$ Since $P\,$ is a polynomial of degree at most $2,\,$ $P\,$ mya have at most two roots.
Acknowledgment
This is problem M392 from the popular Russian magazine Kvant (1977, 03, p 30). The two solutions (1 and 2) are by N. Vasiliev. Amit Itagi (Solution 3) and Roger Mansuy (Solution 4) offerred more mature variants of Solution 2.
The problem is reminiscent of the very first problem that has been discussed at this site, viz., the problem of Four Travelers, that I came across decades ago in Littlewood's Miscellany.
Menelaus and Ceva
- The Menelaus Theorem
- Menelaus Theorem: proofs ugly and elegant - A. Einstein's view
- Ceva's Theorem
- Ceva in Circumscribed Quadrilateral
- Ceva's Theorem: A Matter of Appreciation
- Ceva and Menelaus Meet on the Roads
- Menelaus From Ceva
- Menelaus and Ceva Theorems
- Ceva and Menelaus Theorems for Angle Bisectors
- Ceva's Theorem: Proof Without Words
- Cevian Cradle
- Cevian Cradle II
- Cevian Nest
- Cevian Triangle
- An Application of Ceva's Theorem
- Trigonometric Form of Ceva's Theorem
- Two Proofs of Menelaus Theorem
- Simultaneous Generalization of the Theorems of Ceva and Menelaus
- Menelaus from 3D
- Terquem's Theorem
- Cross Points in a Polygon
- Two Cevians and Proportions in a Triangle, II
- Concurrence Not from School Geometry
- Two Triangles Inscribed in a Conic - with Elementary Solution
- From One Collinearity to Another
- Concurrence in Right Triangle

|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73566701
