Without Definitions: Why $\displaystyle\frac{1}{3}+\frac{2}{5}=\frac{11}{15}?$
Introduction
I have recently run into a 2007 page of mine Why 1/3 + 1/4 = 7/12? The fact that that identity can be established with no resort to any properties of addition, let alone addition of fractions, is, I believe, of a high educational value. For this reason, I have posted the title question on twitter (which was in its infancy in 2007) in the hope of collecting more insights as to why fraction addition works as it does.
I was not disappointed.
Problem

Solution 1
Start with $11$ doughnuts. Cut $5$ into $3$ parts each (part $A)$ and the remaining $6$ do nuts into $5$ parts each (part $B).$ Hand each of $15$ kids one part $A$ and two parts $B.$ Thus each of the $15$ kids gets the same amount and all $11$ do nuts are equitably exhausted.
Solution 2
Arrange $15$ tiles in a $3\times 5$ grid and color as shown below:
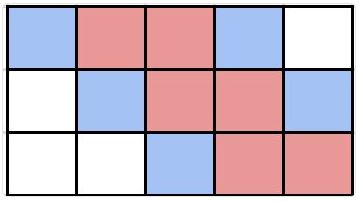
Looking at columns, clearly $\displaystyle\frac{1}{3}$ of the tiles are blue (because each column contain just one blue tile), and at rows, clearly $\displaystyle\frac{2}{5}$ are red (because each row contains exactly two red tiles.) Consider all colored tiles together: $\displaystyle \frac{11}{15}$ are colored.
Solution 3
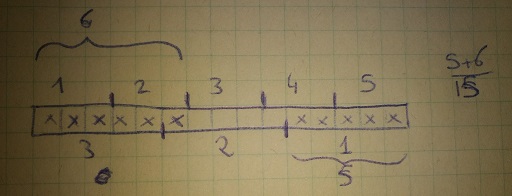
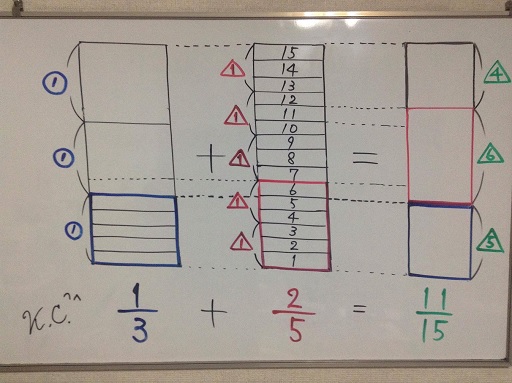
Solution 4
This could be possibly construed as an illustration for Solution 1.
Solution 5
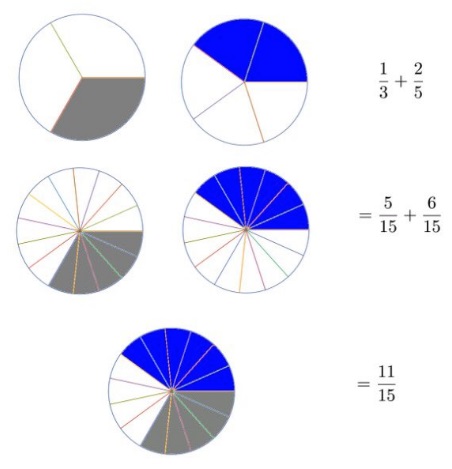
Solution 6

Acknowledgment
This is a follow-up on a much-much older page. Solution 1 is by Amit Itagi; Solution 2 is by Daren Chapin; Solution 3 is by Sergi Pino; Solution 4 is by Kunihiko Chikaya; Solution 5 is by Jim Henegan; Solution 6 is by Max Friedrich Hartmann.
Fractions
- What Is Fraction?
- Operations on Fractions
- Equivalent Fractions
- Fraction Comparison: An Interactive Illustration
- Compare Fractions: Interactive Practice
- Fraction Comparison Sped up
- Counting and Equivalent Fractions
- Product of Simple Fractions
- What's a number? (Rational number in particular)
- Why 1/3 + 1/4 = 7/12?
- Fractions on a Binary Tree
- Fractions on a Binary Tree II
- Archimedes' Law of the Lever
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73554261
