Counting and Equivalent Fractions

Elsewhere we looked into what might be called an organic introduction to addition of fractions. For example, in order to explain why 1/3 + 1/4 = 7/12, we considered the task of dividing 7 apples between 12 boys under the restriction that an apple could be at most cut into 5 equal pieces. The solution was to divides 3 apples into 12 quarters and 4 apples into 12 thirds letting each boy have 1/3 and 1/4 of an apple. Clearly, the procedure leads to all boys having equal amounts. Since there were 7 apples and 12 boys, each of the boys received 7/12 of an apple. The conclusion that 1/3 + 1/4 = 1/12 follows. Curiously, the addition result so expressed has been obtained without any recourse to the definition of the addition of fractions. A close idea can serve to explain the notion of equivalence of fraction.

How many halves are in the whole? Two,One,Two,Three,Four,Many, of course. How many thirds are in the whole? Three,One,Two,Three,Four,Many, of course. What does this say? Very simple: 1 = 2 × 1/2 and 1 = 3 × 1/3.

Now let's count. If, say, one bag contains three apples, in 2 bags there are 6 apples,3 apples,6 apples,9 apples,12 apples; in 3 bags there are 9 apples,3 apples,6 apples,9 apples,12 apples; in 4 bags there are 12 apples,3 apples,6 apples,9 apples,12 apples, and so on. Similarly, in 1 apple there are 3 , 3 , 6 , 9 , 12 thirds; in 2 apples there are 6 , 3 , 6 , 9 , 12 thirds; in 3 apples there are 9 , 3 , 6 , 9 , 12 thirds; in 4 apples there are 12 , 3 , 6 , 9 , 12 thirds. In a concise form, we have

1 = 3 × 1/3, 2 = 6 × 1/3, 3 = 9 × 1/3, 4 = 12 × 1/3.

The first of these means neither more nor less than 1/3 = 1/3; the second tells us that 2/6 = 1/3; next we have 3/9 = 1/3 and 4/12 = 1/3. Let's emphasize those:

1/3 = 1/3, 2/6 = 1/3, 3/9 = 1/3, 4/12 = 1/3.

So there appear to be at least two ways to introduce equivalent fractions.

The more common one is well illustrated with the following problem. A cake cut into 6 pieces is to be divided between three boys. How much will each of the boys receive? Since there are six pieces and three boys, each of the boys will get 2 pieces, i.e. 2/6 of the cake. On the other hand, in the manner described, the three boys have divided evenly one whole cake between themselves, each got 1/3 of the whole, implying that 2/6 = 1/3.

2/6 = 1/3

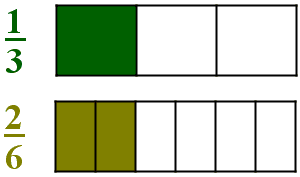
The second approach is to inquire how to divide 2 cakes between 6 boys. A simple way of doing that is to divide the cakes into thirds and give 1/3 of a cake to each boy. Since each of the six boy gets an equal portion of the two cakes we naturally conclude that 1/3 = 2/6.

1/3 = 2/6

In both cases the dark part is a take-home portion of a single boy.

Algebraically, 1/3 is obtained from 2/6 by dividing both the numerator (2) and the denominator (6) of 2/6 by the same number (2). Such an operation is called reduction.

Definition

Dividing the numerator and the denominator of a fraction by their common factor is called reduction.
The operation wherewith both the numerator and the denominator are multiplied by the same number is called expansion.

Both reduction and expansion lead to equivalent fractions. More generally, two fractions are equivalent if both can be reduced to the same fraction:

So, for example, 10/15 = 8/12 because both can be reduced to 2/3: the first with the factor of 5, the second with the factor of 4. The fraction with mutually prime numerator and denominator is said to be in lowest terms. Such a fraction could not be reduced further.

Conversely, expanding the same fraction in two ways produces two equivalent fractions:

Observe, that the so called cross-product gives an identity: (ps)(qt) = (pt)(qs). More generally, we have an important rule:

Two fractions p/q and u/v are equivalent if and only if pv = qu.

From here and the uniqueness of the prime number decomposition, it follows that, among a set of pairwise equivalent fractions, there is a unique one in lowest terms.

Here are additional pages related to the definitions, properties of and operations on, fractions:

Fractions

71548782