Fractions on a Binary Tree

Let a/b be a fraction in lowest terms, where a and b are positive integers, a < b. Place it at the root of a binary tree. Next form its two children a/(a+b) and b/(a+b). Continue this process indefinitely to obtain the following tree diagram.

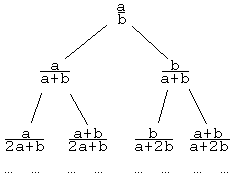
Find a and b such that the diagram starting with a/b contains all positive fractions less than 1.

Solution

References

1. J. Cofman, What To Solve?, Oxford Science Publications, 1996.

• Modular Arithmetic
  • Differences and Similarities
  • Solutions to some problems
• Chinese Remainder Theorem
• Euclid's Algorithm
  • Euclid's Game
  • Binary Euclid's Algorithm
  • gcd and the Fundamental Theorem of Arithmetic
  • Extension of Euclid's Algorithm
  • Stern-Brocot Tree
    • Fine features
    • Binary Encoding
    • Binary Encoding, a Second Interpretation
    • Continued Fractions on the Stern-Brocot Tree
    • Fractions on a Binary Tree
    • Fractions on a Binary Tree II
  • Farey series
    • Farey series, a story
• Pick's Theorem
  • Pick's Theorem, A Proof
  • Farey Series
  • Pick's Theorem Applies to the Farey Series
  • Stern-Brocot Tree
• Fermat's Little Theorem
• Wilson's Theorem
• Euler's Function
• Divisibility Criteria
• Examples
• Equivalence relations
• A real life story

|Contact| |Front page| |Contents| |Algebra|

Solution 1

Let's first show that if the diagram contains all positive fractions, then a/b must be equal to 1/2. Assume, on the contrary, that 1/2 appears somewhere inside the tree. This means that for some p and q either p/(p+q) = 1/2 or q/(p+q) = 1/2. In both cases, p = q = 1 and the direct ancestor of 1/2 - p/q or q/p, as the case may be, equals 1. But 1 can't possibly belong to the tree because the algorithm generates only fractions less than 1.

The algorithm has the property that successors of a fraction in lowest terms are automatically in lowest terms as well. If gcd(p, q) = 1, then too gcd(p, p+q) = 1, since a factor common to both p and (p+q) also divides q.

Assume now that a/b = 1/2 and let p/q be a positive fraction in lowest terms less than 1. We want to show that p/q belongs to the tree. If p/q = 1/2, there is nothing to prove. We have to consider two cases

1. p/q < 1/2
2. p/q > 1/2

In general, for positive fractions r/s less than 1 define the ancestor function A in the following manner: if r/s < 1/2 let A(r/s) = r/(s-r), if r/s > 1/2 let A(r/s) = (s-r)/r.

Starting with r/s, form a sequence of fractions:

(1)	p/q, A(p/q), A(A(p/q)), ...

Observe that the sequence of denominators is decreasing. Therefore, (1) is a finite sequence. Let Aⁿ(p/q) be the last fraction in (1). Its denominator must be 2, for, otherwise, we would be able to continue. So the fraction is 1/2. The function A is called ancestor because it reverses the algorithm that defines the tree. Going backwards, in n steps, we'll get from 1/2 to p/q. Therefore, p/q is on the tree.

Solution 2

In the discussion on the Stern-Brocot tree we defined two functions: f_R(r/s) = r/s+1 = (r+s)/s and f_L(r/s) = r/(r+s). In terms of these two functions, for a given fraction r/s, the algorithm used in the problem generates two descendants: f_L(r/s) and 1/f_R(r/s).

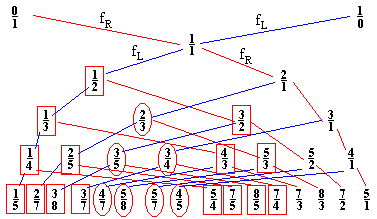
However, by definition,

(2)	1/fR(r/s) = fL(s/r).

Recollect an observation we made in the discussion on the Stern-Brocot tree: f_L transforms a row into the left half of the next row, f_R transforms a row into the right half of the next row. From this remark and (2), it follows that the algorithm fills up the left side of the Stern-Brocot tree, a row at a time. The order of the fractions is, of course, all screwed up. For example, the 4th row will appear as 1/5, 4/5, 3/7, 4/7, 2/7, 5/7, 3/8, 5/8.

An upshot of having two solutions to the problem is that we can interpret Solution 1 as it applies to the Stern-Brocot tree. Unwittingly, we got a second proof that all fractions on the Stern-Brocot tree emerge in lowest terms. We also got a second proof of the fact that the Stern-Brocot tree contains all positive fractions.

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny