Sketch of Second Proof (after Cauchy)

Consider the quantity s(z) = |P(z)|, where

P(z) = a_nzⁿ + a_{n -1}z^{n -1} + ... + a₁z¹ + a₀

is a polynomial of degree n. Clearly, s(z)≠0. If s(z) assumes a global minimum value, say, σ, on C, then it suffices to prove that σ = 0, or equivalently, it suffices to derive a contradiction from the alternative assumption that σ > 0.

Suppose, then, that s(z₀) = σ > 0. It is convenient to "re-center" the arithmetic by setting Q(z) = P(z + z₀ ), so |Q(0)| = |P(z₀ )| = σ, where σ is likewise a global minimum for |Q(z)|.

Expanding out the definition of |Q(z)|, we obtain a set of new coefficients: Q(z) = b_nzⁿ + b_n -1z^n -1 + ... + b₁z¹ + b₀, where b_n = a_n≠0, and b₀ = P(z₀ )≠0. Let m be the exponent of the lowest power of z in Q(z) whose coefficient b_m is not zero. Now consider the behavior of Q(z) for points z whose absolute value is very small, say the points z = lying on a small circle centered at the origin of radius ρ. As observed above, as z sweeps once around this small circle, Q(z) closely approximates the behavior of b_mz^m + b₀, which sweeps out a small circle (of radius |b_m|ρ^m) around the point b₀ = P(z₀ ). (In fact, Q(z) sweeps around this circle m times.) By choosing ρ sufficiently small, we may ensure that the radius of this circle (that is, the magnitude of Q(z) - b₀) is smaller than σ. Such a circle will necessarily intersect the line segment connecting the origin to the point b₀ = P(z₀ ), at a point, say Q(z₁ ), nearer the origin than b₀ = P(z₀ ). But then |Q(z₁ )| = |P(z₁ + z₀ )| <σ, contradicting our choice of σ as a global minimum of s(z) = |P(z)|. (Actually, Q(z) may only lie near this circle, not on it. Fortunately, the discrepancy consists of the remaining terms of Q(z) (if any), all of which contain powers of ρ higher than m. By taking ρ even smaller, if necessary, we can guarantee that this discrepancy does not wreck the geometry - see Figure 5.)

Figure 5.Behavior of Q(z) for "small" values of z. If z lies on the small circle of radius ρ centered at the origin of the z-plane, then Q(z)≈b_mz^m + b₀, which is the larger circle in the figure, centered at Q(0) = b₀, with radius |b^m|ρ^m. For ρ sufficiently small, the remaining terms of (if any) of Q(z) sum to a vector whose magnitude (proportional to ρⁿ, n >m, is less than the radius of the smaller circle in the figure.) As z sweeps out the small circle of radius ρ on the z-plane, the locus of Q(z) loops around Q(0) = b₀ (in fact, m times), and necessarily intersects the vector drawn from the origin of the w-plane to Q(0).

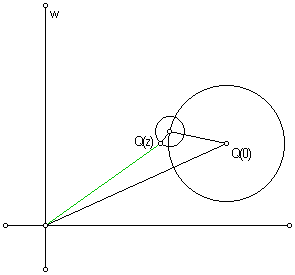
Thus the assumption that σ > 0 is untenable, and we conclude that σ = 0, that is, that P(z) has a complex root.

71616326