---

Yet Another Proof of the Fundamental
Theorem of Algebra

---

R. P. Boas, Jr.

---

The following proof of the fundamental theorem of algebra by contour integration is similar to Ankeny's [1], but is simpler because it uses integration around the unit circle (which is usually the first application of contour integration) instead of integration along the real axis; thus there is no need to discuss the asymptotic behavior of any integrals.

Let P(z) be a nonconstant polynomial; we are to show that P(z) = 0 for some z. We may suppose P(z) real for real z. (Indeed, otherwise let be the polynomial whose coefficients are the conjugates of those of P(z) and consider .) Suppose then that P(z) is real for real z and is never 0; we deduce a contradiction. Since P(z) does not either vanish or change sign for real z, we have

(1)

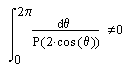
But this integral is equal to the contour integral

(2)

where Q(z) = zⁿP(z + z^-1) is a polynomial. For z ≠ 0, Q(z)≠0; in addition, if a_n is the leading coefficient in P(z), we have Q(0) = a_n ≠0. Since Q(z) is never zero, the integrand in (2) is analytic and hence the integral is zero by Cauchy's theorem, contradicting (1).

Reference

1. N.C. Ankeny, One more proof of the fundamental theorem of algebra, this Monthly, 54 (1947) 464.

• Perfect numbers are complex, complex numbers might be perfect
• Fundamental Theorem of Algebra: Statement and Significance
• What's in a proof?
• More about proofs
• Axiomatics
• Intuition and Rigor
• How to Prove Bolzano's Theorem
• Early attempts
• Proofs of the Fundamental Theorem of Algebra
  • Remarks on Proving The Fundamental Theorem of Algebra
    • Sketch of a Proof by Birkhoff and MacLane
    • Sketch of Second Proof (after Cauchy)
    • Details of the Cauchy's Proof
    • Note on the Extreme Value Theorem
    • Sketch of Proof by the methods of the theory of Complex Variables (after Liouville)
    • Maximum Modulus Theorem
  • A Proof of the Fundamental Theorem of Algebra: Standing on the shoulders of giants
  • Yet Another Proof of the Fundamental Theorem of Algebra
  • Fundamental Theorem of Algebra - Yet Another Proof
  • A topological proof, going in circles and counting
  • A Simple Complex Analysis Proof
  • An Advanced Calculus Proof

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny