|
|
|
|
|
|
|
|
A topological proof
|
| f(z) = an z n + an -1 z n -1 + ... + a1z1 + a0 |
has no root, so that for every complex number z
| f(z) ≠ 0. |
On this assumption, if we now allow z to describe any closed curve in the
 | |
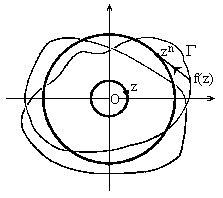| Proof of fundamental theorem of algebra. |
We may, therefore, define the order of the origin O with respect to the function f(z) for any closed curve C as the net number of complete revolutions made by an arrow joining O to a point on the curve Γ traced out by the point representing f(z) as z traces out the curve C. As the curve C we shall take a circle with O as center and with radius t, and we define the function φ(t) to be the order of O with respect to the function f(z) for the circle about O with radius t. Clearly
It remains only to show that φ(t) = n for large values of t. We observe that on a circle of radius
| t > 1 and t > |a0| + |a1| + … + |an - 1|, |
we have the inequality
| |f(z) - z n| = |an-1 z n-1 + an-2 z n-2 + … + a0| ≤ |an-1||z|n-1 + |an-2||z|n-2 + … + |a0| = tn-1[|an-1| + … +|a0| /tn-1] ≤ tn-1[|an-1| + … +|a0|] < tn = |z|n. |
Since the expression on the left is the distance between the two points zn and f(z), while the last expression on the right is the distance of the point zn from the origin, we see that the straight line segment joining the two points f(z) and zn cannot pass through the origin so long as z is on the circle of radius t about the origin. This being so, we may continuously deform the curve traced out by f(z) into the curve traced out by zn without ever passing through the origin, simply by pushing each point f(z) along the segment joining it to zn. Since the order of the origin will vary continuously and can assume only integral values during this deformation, it must be the same for both curves. Since the order for zn is n, the order for f(z) must also be n. This completes the proof.
Reference
- R.Courant and H.Robbins, What is Mathematics?, Oxford University Press, 1966.
- Perfect numbers are complex, complex numbers might be perfect
- Fundamental Theorem of Algebra: Statement and Significance
- What's in a proof?
- More about proofs
- Axiomatics
- Intuition and Rigor
- How to Prove Bolzano's Theorem
- Early attempts
- Proofs of the Fundamental Theorem of Algebra
- Remarks on Proving The Fundamental Theorem of Algebra
- A Proof of the Fundamental Theorem of Algebra: Standing on the shoulders of giants
- Yet Another Proof of the Fundamental Theorem of Algebra
- Fundamental Theorem of Algebra - Yet Another Proof
- A topological proof, going in circles and counting
- A Simple Complex Analysis Proof
- An Advanced Calculus Proof
| 33068555 |  |
