Details of the Proof by Cauchy
The task of wrestling this idea into a respectable proof has flustered a good many authors. For the sake of completeness, I paraphrase the best version I have yet found, from JMH Olmsted, Advanced Calculus Appleton Century Crofts, 1961, p 516:
Express the complex number -b0/bm in the form -b0/bm = ![]() , and let
, and let
![]() . Let z1 =
. Let z1 = ![]() ,
where r is yet to be determined. Then for the dominant term under conditions of small
r we have
,
where r is yet to be determined. Then for the dominant term under conditions of small
r we have
![]() .
.
We may thus rewrite Q(z1 ) in the form
![]() .
.
Taking absolute values, and applying the triangle inequality, we have

We now choose r so small that the quantity [|b|m+1r + ... + |bn|rn-m] < |b0|/t, and also so small that rm<t (so that |t - rm| = t - rm). Then
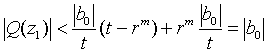
This contradicts the assumption that
![]() = |b0| is the
global minimum value for Q(z), QED.
= |b0| is the
global minimum value for Q(z), QED.
"But, that s(z) = |P(z)| assumes a global minimum value over C, we must prove thus." [I am here paraphrasing Euclid. The climactic conclusion of Euclid’s Elements is the construction of the five regular solids (tetrahedron, cube, octahedron, icosahedron and dodecahedron), and the demonstration that there can be no others (XIII. 18). There follows the anticlimactic proposition "But that the angle of the equilateral and equiangular pentagon is a right angle and a fifth we must prove thus." Apparently, in the age of papyrus (before word-processing software), it was not so easy to repair an error of omission by inserting the material back at a more natural location.]
It is not true in general that the absolute value of a continuous (or even differentiable) function over C assumes a global minimum – in this regard, polynomials are special. For example, the exponential function ez = ex+iy = ex(cos(y) + isin(y)), which, we have already observed, has no roots over C, has magnitude |ex+iy| = ex, which is asymptotic to its greatest lower bound (0), but which never assumes 0 as a value.
In order to demonstrate that the absolute value of the polynomial P(z) assumes its minimal value, we examine its behavior for large |z|, as well as invoke the Extreme Value Theorem as applied to a real-valued function on a closed disk in C.
We have P(z) = anz n + an -1z n -1 + ... + a1z1 + a0. Factoring out zn, the highest power of z, we have P(z) = zn(an + an -1z -1 + ... + a1z1-n + a0z-n). Taking absolute values, |P(z)| = |zn||an + an -1z -1 + ... + a1z1-n + a0z-n|. Now choose R sufficiently large that for each j<n,
| (*) |

|
whenever |z| > R.
Then for |z| > R, |an + an -1z -1 + ... + a1z1-n + a0z-n|≥|an|/2, and |P(z)| > Rnan /2 (See Figure 6.)
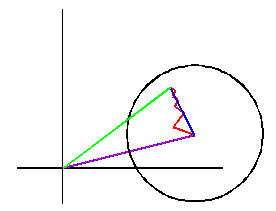
Behavior of |an + an-1z-1 + ... + a0z-n| for large |z|. an is shown as the purple vector drawn from the origin. The remaining terms form the red zig-zag, whose vector sum is drawn in blue. By taking |z| suffciently large, this vector sum can be guaranteed to be smaller in magnitude than |an|/2, the radius of the circle with center at an, ensuring that |an + an-1z-1 + ... + a0z-n| for large |z| (the magnitude of the vector drawn in green) is at least |an|/2.
Now choose any z2 such that |P(z2)| = u > 0. Choose R > 2(1 + u)/|an|, or larger, so that (*) is simultaneously satisfied . Then for |z| > R, we have |P(z)| > u.
Clearly, the minimal value, if any, of |P(z)| on the closed disc |z| ≤ R is the global minimum of |P(z)|, since |P(z2)| = u, but |P(z)| > u outside this disc.
Now apply the Extreme Value Theorem to conclude that |P(z)| assumes a minimal value on the closed disc |z| ≤ R, which is a compact set. Then this minimal value is the global minimal value for |P(z)| over the entire complex plane, QED.
- Perfect numbers are complex, complex numbers might be perfect
- Fundamental Theorem of Algebra: Statement and Significance
- What's in a proof?
- More about proofs
- Axiomatics
- Intuition and Rigor
- How to Prove Bolzano's Theorem
- Early attempts
- Proofs of the Fundamental Theorem of Algebra
- Remarks on Proving The Fundamental Theorem of Algebra
- A Proof of the Fundamental Theorem of Algebra: Standing on the shoulders of giants
- Yet Another Proof of the Fundamental Theorem of Algebra
- Fundamental Theorem of Algebra - Yet Another Proof
- A topological proof, going in circles and counting
- A Simple Complex Analysis Proof
- An Advanced Calculus Proof
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73580334
