Sketch of a Proof by Birkhoff and MacLane

Consider the polynomial P(z) as a mapping from one copy of the complex plane (say, the z-plane) to another copy of the complex plane (say, the w-plane). Such a mapping transforms a circle |z| = r of radius r into a closed curve on the w-plane (see Figure 1). For very large values of r, the a_nz ⁿ term dominates, and the image is a closed curve which loops n times around the origin of the w-plane (see Figure 2). On the other hand, for very small values of r, we may neglect all the terms except a_mz ^m + a₀, where a_m is the coefficient with the lowest index m>0 which is not equal to zero, and the image loops m times around the point w = a₀ (Figure 3). As r0, the image collapses to the point a₀. We now invoke the topological fact that if we start with r very large, and continuously reduce r to 0, simultaneously reducing the image in the w -plane from a large loop encircling the origin (likely more than once) to a point, we must necessarily encounter a stage where the image curve passes through the origin w = 0. Thus, we have shown that some point on the z-plane maps to w = 0 - that is, that there is a complex root of P(z). (For details, see Birkhoff & MacLaine, A Survey of Modern Algebra, AK Peters, 1997)

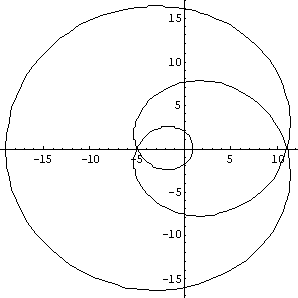
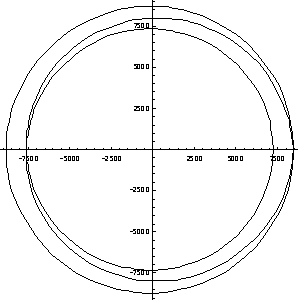
Figure 1. Image of circle |z| = 2 under the mapping P(z) = z3 - 2z2 + z - 1.	Figure 2. Image of circle |z| = 20 under the mapping P(z) = z3 - 2z2 + z - 1.
Figure 3. |z| = 0.1 under the mapping P(z) = z3 - 2z2 + z - 1. Note the enlarged scale.	Figure 4. Image of circle |z| = 0.75 under the mapping P(z) = z3 - 2z2 + z - 1. Apparently a root of this polynomial lies very near this circle.

• Perfect numbers are complex, complex numbers might be perfect
• Fundamental Theorem of Algebra: Statement and Significance
• What's in a proof?
• More about proofs
• Axiomatics
• Intuition and Rigor
• How to Prove Bolzano's Theorem
• Early attempts
• Proofs of the Fundamental Theorem of Algebra
  • Remarks on Proving The Fundamental Theorem of Algebra
    • Sketch of a Proof by Birkhoff and MacLane
    • Sketch of Second Proof (after Cauchy)
    • Details of the Cauchy's Proof
    • Note on the Extreme Value Theorem
    • Sketch of Proof by the methods of the theory of Complex Variables (after Liouville)
    • Maximum Modulus Theorem
  • A Proof of the Fundamental Theorem of Algebra: Standing on the shoulders of giants
  • Yet Another Proof of the Fundamental Theorem of Algebra
  • Fundamental Theorem of Algebra - Yet Another Proof
  • A topological proof, going in circles and counting
  • A Simple Complex Analysis Proof
  • An Advanced Calculus Proof

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny