Treasure Hunt in a Square Grid

The so-called taxicab or city-block distance is at the heart of a computer game "Treasure Hunt" developed by math educator and researcher Tom O'Brien, also known under the nom de plume of Professor Tobbs. The game is to teach elementary school students logical thinking. The goal of the game is to find a treasure hidden under one of the squares in a 4×4 grid. The way to locate the treasure is by touching a square on the grid. If you are lucky to stumble on the square that conceals the treasure the game stops. Otherwise, you are given a clue - the taxicab distance from the selected square to the treasure. You may touch as many squares as you need to solve the puzzle.

The game was described at the Bogglers section of the Discover Magazine, where two challenging problems have been posted related to the Treasure Hunt game:

What is the greatest number of squares you can touch and still not be able to determine for certain where the treasure is?
What is the best strategy for finding the treasure? In other words, how few squares can you touch and still be sure to find the treasure?

The applet below helps you experiment with locating the treasure, practice computing the taxicab distance and answer the two questions.

It also allows you to change the size of the board to 8×8. See if that complicates the game.

alt="Your browser understands the <APPLET> tag but isn't running the applet, for some reason." Your browser is completely ignoring the <APPLET> tag!

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

Problem 1

What is the greatest number of squares you can touch and still not be able to determine for certain where the treasure is?

Answer

10! This is demonstrated by the following layout:

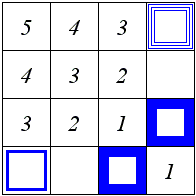
The Discover Magazine gives an underestimate of 4 based on the following layout:

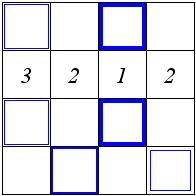
Problem 2

What is the best strategy for finding the treasure? In other words, how few squares can you touch and still be sure to find the treasure?

Answer

For this problem the Discover Magazine gives a correct, albeit incomplete, answer:

Two squares are always enough. First touch a corner square. The number will reveal which diagonal the treasure lies on. (A 2 in the top left corner square would show that the treasure is on the diagonal that runs from the third square in the top row to the third square in the first column.) Then touch a square at one end of the diagonal. This will tell you where along the diagonal the treasure is hidden.

The proof that touching a corner square reveals a diagonal that houses the treasure is pretty simple, two words actually, but should be given. (I give it elsewhere.) As the whole exercise is intended for the young children who only began developing the facility for inference, I would use this opportunity to let (and help) them employ the inference.

Secondly, the solution the magazine offers is correct and works every time. There is another one that appears to me more congenial to mathematical thinking than the magazine's. Indeed, if touching one corner reveals a diagonal, touching another corner also reveals a diagonal. If the two corners are adjacent, the corresponding diagonals are crossing each other. The cell where they cross is bound to contain the treasure.

Taxicab/City-block Distance.

Treasure Hunt in a Square Grid
Treasure Hunt from Outside the Grid
Objects distant and near
Farmer and Wife To Catch Rooster and Hen
Distance Formula
What Is Geometry?

41143667