Seven Circles Theorem

The applet below illustrates the Seven Circles Theorem:

The theorem is of a recent origin and first appeared in [Evelyn, Money-Coutts, Tyrrell, pp. 31-42]. (The 68 pages book is now a bibliographical rarity and can be had for a lofty price of about $500 - give or take a few cents.) A trigonometric proof has been published by H. Martin Cundy in 1978 and a practically elementary proof by Stanley Rabinowitz in 1975.

Solution

References

1. H. M. Cundy, The Seven-circles Theorem, Math. Gazette. 62(1978) 200–203.
2. C. J. A. Evelyn, G. B. Money-Coutts, J. A. Tyrrell, The seven circles theorem and other new theorems , Stacey International (1974), pp. 31-42
3. S. Rabinowitz, The Seven Circles Theorem, Pi Mu Epsilon Journal, 8(1987) 441-449

|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|

The first step in the proof is a lemma found in [Coxeter] which Rabonowitz dubbed Ceva's Theorem for Chords.

(1)	AB · CD · EF = BC · DE · FA.

Proof

First assume that the six points are such that the chords AD, BE, CF concur in point P. Observe the presence of three pairs of similar triangles. (In the diagram one pair is highlighted and pairs of equal angles are shown. One pair is of central angles; two pairs are inscribed subtended by the same arc.)

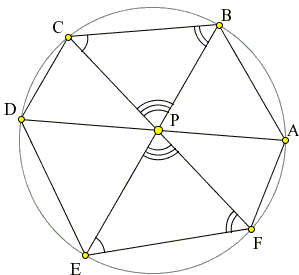
From similar triangles, we get the proportions:

AB/DE = PA/PE
CD/FA = PC/PA
EF/BC = PF/PB
PC/PE = PB/PF.

Multiplying these together gives us the desired result.

In the other direction, suppose (1) holds but the chords do not concur. Of the three arcs ABC, CDE, EFA, at least one must be smaller than a semicircle. Let it be the arc CDE. Denote P the intersection of BE and CF. Let X be the second point of intersection of AP with the circle.

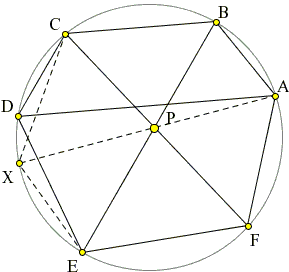
By the above,

Which compared to (1) gives

If X and D are different then, say, CX > CD. But then XE < DE, so that CX / XE > CD / DE and (2) can't hold. A contradiction. Therefore, X = D and the three chords indeed concur.

The second step in the proof is the following

Lemma 2

Let two externally tangent circles, (P) and (Q), be internally tangent to circle (C) at points A and B respectively. If the radii of circles (C), (P), and (Q) are R, p, and q, respectively, then

AB² = 4R² f(p)·f(q),

where f(x) = x / (R - x).

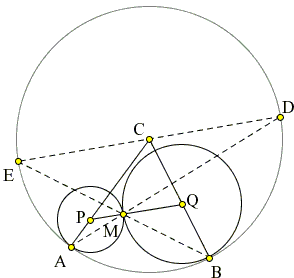
Proof

Triangles APM and ACD are isosceles with a common base angle at A. It follows that their other base angles (at M and D) are also equal. Therefore, CD||MP. Similarly, CE||MQ. But PMQ is a straight line and then so is DCE.

Observe also that, as inscribed angles subtended by the same arc,

∠EBA = ∠EDA and
∠BAD = ∠BED.

It follows there are three pairs of similar triangles: APM/ACD, BQM/BCE, and ABM/EDM which gives the following proportions:

AB/DE = AM/EM = BM/DM.

But DE = 2R. Thus we have

AB/2R · AB/2R	= AM/EM · BM/DM
	= AM/EM · BM/DM
	= AM/DM · BM/EM
	= AP/CP · BQ/CQ
	= p(R - p) · q(R - q).

Proof of the Seven Circles Theorem

Assume the points of tangency of circle C with circles S_k are A_k, and that r_k denotes the radius of S_k, k = 1, 2, ..., 6. By Lemma 2,

k = 1, 2, ..., 6, and r₇ = r₀. It follows that

which of course implies

and by Lemma1 the three chords A₀A₃, A₁A₄, A₂A₅ are concurrent.

The applet shows that the concurrency takes place in other configurations as well. For example, circles S_k may all be tangent to circle C externally. The above proof goes through in this case if the function f(x) is redefined: f(x) = x/(R + x).

In a special case where circles S₁, S₃, S₅ expand into straight lines, the configuration becomes that of the incircle of a triangle with three additional circles inscribed into curvilinear triangles cut off by the incircle. If the radii of the latter shrinks to 0, the remaining points of tangency are none other than the intouch points and the point of concurrency is the point of Gergonne.

As can be grasped from the diagrams below, the theorem holds in a more general setting where the points of tangency A_k do not form a convex hexagon.

   

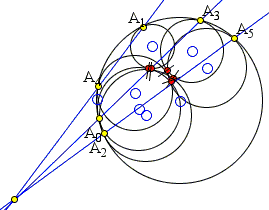
References

1. H. S. M. Coxeter, Problem 527, The Mathematics Student 28 (1980) 3.

|Activities| |Contact| |Front page| |Contents| |Geometry| |Eye opener| |Store|