Representation of numbers with three 3's

Remark: To simplify expressions, let's agree on the following notations that designated quantities expressible with a single 3:

• {1} = [√3] = 1
• {2} = [√3!] = 2
• {50} = [√√√√√√√√√√((3!)!)!] = 50

  For example, {1}·{2} + 3 stands for [√3]·[√3!] + 3 = 5.

  1	√3·√3/3
  2	3 - 3/3 = (3 + 3)/3
  3	3·3/3 = 3 + 3 - 3
  4	3 + 3/3
  5	3!/3 + 3
  6	3!·3/3 = 3/.(3) - 3 = 3<<(3/3)
  7	3! + 3/3 = 3/.3 - 3
  8	[3·√3 + 3]
  9	3 + 3 + 3 = 33/3
  10	[(√3 + √3)·3] = (3·3)^3
  11	33/3
  12	3! + 3 + 3 = 3·3 + 3 = 3/.(3) + 3 = (3!)!/(3!)!! - 3
  13	3/.3 + 3
  14	[3·(√3 + 3)]
  15	3·3! - 3 = (3! - 3/3)!! = [3·3·√3] = (3! - [3/√3])!!
  16	[3·3! - √3]
  17	3!/.3 - 3 = 3·3! - [√3]
  18	(3 + 3)·3 = (3!)!/(3!)!! + 3
  19	[3!√3] - 3 = (3!)!!/3 + 3
  20	(3 + 3)/.3
  21	3·3! + 3
  22	[[3! - √3]!! - √3]
  23	[3! - √3]!! - [√3]
  24	[3! - 3/√3]!!
  25	[3! - √3]!! + [√3]
  26	[[3! - √3]!! + √3]
  27	3·3·3
  28	33 + [√3]
  29	[(3!)!!/√3 + √3]
  30	33 + 3 = (3!)!! - 3·3! = 3/.([√3]) + 3
  31	3/.[√3] + [√3]
  32	33 - [√3](1)
  33	33 + 3!(1)
  34	33 + [√3]
  35	33 + [√3!](1)
  36	33 + 3
  37	[√(√(3!)!]!/3 - 3(1)
  38	33 + [√(√(3!)!)](1)
  39	33 + 3!(1)
  40	(3!)!/3!/3(1)
  41	[√(√(3!)!]!/3 + [√3](1)
  42	[√(√(3!)!]!/3 + [√3!](1) = (3!)!! - 3 - 3
  43	[√(√(3!)!]!/3 + 3(1)
  44	{50} - 3 - 3(2)
  45	[√(√(3!)!]!/3 + [√(√(3!)!](1) = {50} - {2} - 3(2)
  46	[√(√(3!)!]!/3 + 3!(1) = {50} - {2} - {2}(2)
  47	{50} - 3! - 3(2) = {50} - {1} - {2} = (3!)!! - 3/3
  48	{50} - 3!/3(2) = {50} - {1} - {1} = (3!)!!/3·3 = (3!)!! + 3 - 3
  49	{50} - 3/3(2) = (3!)!! + 3/3
  50	{50} - 3 + 3(2) = (3!)!! + 3!/3
  51	{50} + 3/3(2) = (3!)!! + Ö3·Ö3
  52	{50} +3!/3(2) = {50) + 3!/3
  53	{50} + 3! - 3(2) = {50) + 3! - 3
  54	{50} + {2} + {2}(2) = (3!)!! + 3 + 3
  55	{50} + {2} + 3(2)
  56	{50} + 3 + 3(2)
  57	{50} + 3! + {1}(2) = (3!)!! + 3·3
  58	{50} + 3! + {2}(2) = {50} + {2}3 = {50} + (3!)!!/3! = (3!)!! + 3/.3
  59	{50} + 3·3(2) = {50) + 3! + 3
  60	{50} + 3/.3(2)
  61	[√((((√3!)!)!)!) - 33](3)
  62	{50} + 3! + 3!
  63	[{50} + √(3!)!! + √(3!)!!]

  (¹) By Andre Gustavo dos Santos from Brasil

  (²) By Ken Nisbet, Crail, Fife, Scotland

  (³) By Ken Nisbet, Crail, Fife, Scotland. Ken's formula depends on the extension of the factorial n! to arguments other than natural numbers. The extension is known as the G function. For natural x, G(x+1) = x!. In general, G(x+1) = xG(x). The G function is defined by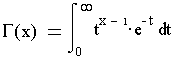

  

  where x could be complex with the real part greater than 0.

  
  

  Related material Read more...
  	Funny Arithmetic
  	A single formula to express all numbers
  	Any Integer with Three 2s
  	Representation of numbers with a single 4. The rules and the possibilities
  	One 4, a story
  	Three 3's
  	Representation of numbers with three 4's
  	Representation of numbers with three 5's
  	Representation of numbers with four 3's
  	Representation of numbers with four 4's
  	Representation of numbers with four 5's
  	A problem of representing 4 by four identical digits
  	A problem of representing 6 by three identical digits
  	A 9's Fan's Clock
  	Make an Identity
  	Fun with numbers: place plus/minus signs between the digits
  	24 with One Digit
  	Representation of 3 with Three Equal Digits

  

  |Contact| |Front page| |Contents| |Up| |Arithmetic|

   

  Copyright © 1996 - 2015 Alexander Bogomolny