Orthocenter in Complex Plane
What is this about?
21 January 2016, Created with GeoGebra
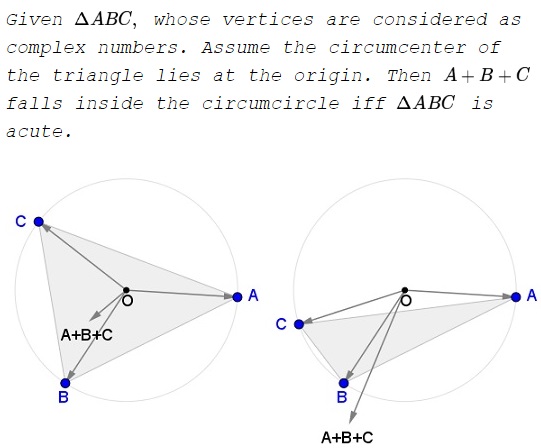
Problem
Proof
We know that, for a triangle with the circumcenter at the origin, the sum of the vertices coincides with the orthocenter. The orthocenter is known to fall outside the triangle if the triangle is obtuse. In this case, the orthocenter lies in the vertical pair of the obtuse angle:
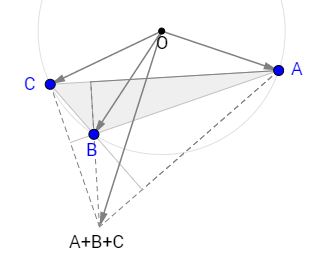
It's thus clear that it also falls outside the circumcircle.
Acknowledgment
The idea of this page came up in a discussion with Leo Giugiuc of another problem.
Complex Numbers
- Algebraic Structure of Complex Numbers
- Division of Complex Numbers
- Useful Identities Among Complex Numbers
- Useful Inequalities Among Complex Numbers
- Trigonometric Form of Complex Numbers
- Real and Complex Products of Complex Numbers
- Complex Numbers and Geometry
- Plane Isometries As Complex Functions
- Remarks on the History of Complex Numbers
- Complex Numbers: an Interactive Gizmo
- Cartesian Coordinate System
- Fundamental Theorem of Algebra
- Complex Number To a Complex Power May Be Real
- One can't compare two complex numbers
- Riemann Sphere and Möbius Transformation
- Problems
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73559455
