Area of Parallelogram
The area of a rectangle equals the product of its sides. The area of a parallelogram equals the product of one of its sides times the distance between that side and its parallel (and equal) mate.
| What if applet does not run? |
It's customary to base a demonstration for the area of a parallelogram formula on Figure 1 below:
| (1) | Area(ABCD) | = Area(AFD) + Area(DFBC) |
| = Area(BGC) + Area(DFBC) | ||
| = Area(DFGC). |
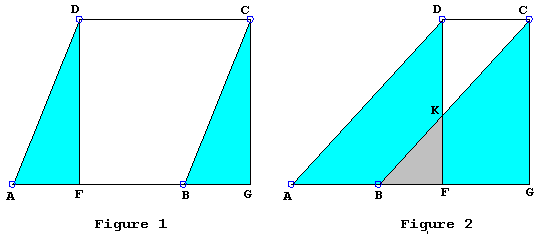
This demonstration is incomplete as it fails to account for the possibility depicted in Figure 2, apparently not accounted for in the above derivation. There are at least three ways to rectify the situation.
We may use brute force [Eves, p. 160] to handle Figure 2 separately of Figure 1:
| (2) | Area(ABCD) | = Area(DKC) + Area(AFD) - Area(BFK) |
| = Area(DKC) + Area(BGC) - Area(BFK) | ||
| = Area(DFGC). |
We may also notice that, when the quadrilateral DFBC consists of two triangles DKC and BKF, the orientation of only one of them matches that of DFBC. For example, in Figure 2, the orientation of DFBC is counterclockwise and so is the orientation of DKC, whereas the orientation of BKF induced by that of DFBC is clockwise. We may then agree to consider the signed areas, ascribing negative areas to the clockwise oriented shapes. With this convention, (2) reduces to (1).
The third approach is more elementary. One of the rather more salient shapes in Figure 2 is the trapezoid AGCD. We may observe that
| (3) | Area(ABCD) | = Area(AGCD) - Area(BGC) |
| = Area(AGCD) - Area(AFD) | ||
| = Area(DFGC). |
Corollary
Triangles ABD and ACD are reflections of each other in the center - the point of intersections of the diagonals - of the parallelogram. They are therefore always equal as are their areas. The area of each then is half that of the parallelogram. The above leads to the formula:
Area of triangle = base × height /2.
(Another demonstration follows by equidecomposition. There is also a more common one.)
References
- H. Eves, Mathematical Reminiscences, MAA, 2001
A letter from Scott Brodie reminded me of Heath's commentary on Euclid's Elements.
| Subject: | Area of parallelograms |
|---|---|
| Date: | Sun, 30 Jun 2002 15:55:05 -0400 |
| From: | Scott E. Brodie |
Hi, Alex --
It is instructive (as usual!) to compare the modern textbook treatment to Euclid (I.35). Euclid gives only your Figure 2 (though to be sure, upside-down). This is a good, if simple, example of his frequent practice (according to Heath) of generally setting out only the most difficult case -- a far cry from our modern textbooks, which seem to typically treat the easiest case, and leave the rest to the reader, if they do not omit it entirely!
Best regards,
Scott.
Commenting on I.35, Heath says in particular,
...
As is well known, Simson (after Clairaut) slightly altered the proof in order to make it applicable to all the three possible cases. The alteration substituted one step of subtracting congruent areas (the triangles AFD, BGC) from one and the same area (the trapezium AGCD) for the two steps above shown of first subtracting and then adding a certain area.
...
As usual, Proclus, observing that Euclid has given only the most difficult of the three possible cases, adds the other two with separate proofs.
...
Proclus observes that the present theorem and the similar one relating to triangles are among the so-called paradoxical theorems of mathematics, since the uninstructed might well regard it as impossible that the area of the parallelograms should remain the same while the length of the sides other than the base and the side opposite to it may increase indefinitely.
I find it amazing that the simplification mentioned by Heath was not found until the 18th century.
Later on, Douglas Rogers offered (private communication, June, 2007) his insights concerning Euclid's approach to I.35 which appears to merit an additional commendation:
Alex,
Now, I wonder whether you have considered Elements I.35, that parallelograms on the same base and between the same parallels are equal in area? If so, then you may know that there has been a deal of sniping about Euclid's argument by commentators down the centuries, with discussion of different cases.
I am afraid that I do not see this at all. Let us agree that in the parallelograms ABCD and EBCF on the common base BC and with A, D, E, F on a parallel line to BC that A comes first in reading from left to right along that line. If we have genuinely different parallelograms, then BE and CD are not parallel, so meet, say at G. It is of no matter whether G is between the parallel lines or not.
In all cases, we have the dissections of the parallelograms into pairwise congruent triangle which variously overlap or are juxtaposed with one another:
ABCD = EAB + CBG - EDG;
EBCF = FDC + CBG - EDG.
The main objection seems to be that Euclid is only treating the case where AD is disjoint from EF, although it is conceded that this is the most difficult case. However, we now see that this is far from the case. It is important to recall that, up to this point, Euclid has only been treating equality of areas in terms of congruence of triangles, so, if he is to extend the definition of equality of area to other polygonal regions, no doubt he felt he needed to stick with triangles, juxtaposing, overlapping, or cutting them off; and, as we see from the above dissections, he can always do that, although maybe he does have to be careful not to remove something before it is there, which is why I have put the addition (juxtaposition) before the subtraction (cutting off or overlapping).
But suppose that the case is still pressed that we should consider AD and EF overlapping separately from when they are disjoint, because then G is not between the parallel lines. Then the triangles BCD and BCF are in exactly the same positions as those Euclid considers in I.37, where he moves to the parallelograms ABCD and, not EBCF, but rather FBCE' where now AD and FE' are equal but disjoint - of course, the triangles EFB, FE'C and CBF are all congruent. So, this suggests that Euclid is well aware that, even if it might seem that there are two cases, one can always be converted to the other by what has been established prior to I.35.
- What Is Area
- Elementary Introduction into the Concept of Area
- Area of Rectangle
- Area of Parallelogram
- Area of Triangle
- Area and Perimeter of Circle
- Equidecomposition of a Triangle and a Rectangle: first variant
- Pick's Theorem
- Area of a Circle by Rabbi Abraham bar Hiyya Hanasi
- Area of a Circle by Leonardo da Vinci
- Volume and Area of Torricelli's Trumpet
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73373002
