Elementary Introduction into the Concept of Area
Area, as many other mathematical concepts, has experiential origins. Intuitively, this is the measure of expanse associated with plane figures. Area is a \(2\)-dimensional analogue of the \(1\)-dimensional length and \(3\)-dimensional volume.
Paint containers carry a mention of the area the paint should suffice to cover. Area of a forest region is an indicator of the number of trees that grow there, and vice versa.
As many other mathematical concepts, area can be defined in a variety of ways. The context and potential applications may dictate which of the possible definitions is preferable under given circumstances.
Square is definitely a most fundamental notion where the areas are concerned. This is reflected in the units that are used to measure or describe area: $\mbox{in}^{2},$ $\mbox{cm}^{2},$ $\mbox{mi}^{2},$ and so on. Regardless of which axioms are chosen to develop mathematical properties of area, the area of a unit square, i.e., a square whose side length is $1$ unit is always 1 square unit. However, depending on the selection of axioms, this may be either a theorem or an axiom itself. (Note that the words "square unit" are often omitted where it's not important which units are actually used.)
Two axioms are universally included: the first simply asserts to that concept of area makes sense, the second is that the area is additive on a set of polygons:
Axiom 1
Congruent shapes have equal areas.
Axiom 2
If a polygon is split into a finite number of polygons then its area is the sum of the areas of the pieces it is split into.
From these two axioms it is possible to deduce that the area of a rectangle is proportional to the product of its side lengths. For convenience, let $S(P)$ denote the area of shape $P.$ $S$ is therefore a function on the set of plane shapes. Then $S(ABCD)=AB\times BC.$
We could have formulated that differently: the area of a rectangle is the base times the height. In this form, the statement also holds for parallelogram. This could be seen from the diagram below, where a triangle in a parallelogram is cut off at one side and added at another to form a rectangle.
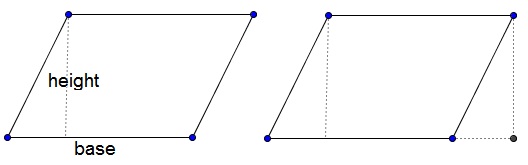
(In reality the situation is a little more complex than that.) If we denote the base $b$ and the height $h$ then $S=bh$ is a valid formula for the area of both rectangle and parallelogram.
The area of a triangle is half that: half the product of the base and the altitude, $\displaystyle\frac{1}{2}bh:$
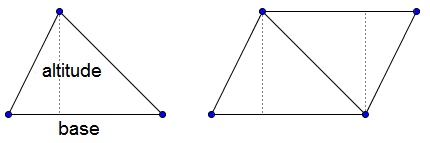
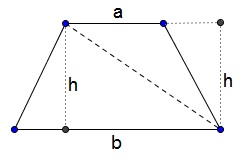
A trapezoid can be cut into two triangles with different bases but the equal altitudes, so its area is $\displaystyle\frac{1}{2}ah+\frac{1}{2}bh=\frac{a+b}{2}h:$
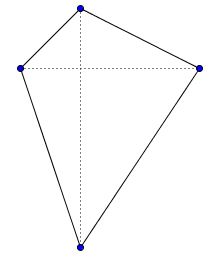
For a kite, we split it also into two triangles by one of the diagonals that serves the base for both and divides the other diagonal into the altitudes of the two triangles, $\displaystyle\frac{1}{2}dg +\frac{1}{2}dh=\frac{1}{2}d(g+h)=\frac{1}{2}de,$ half the product of the diagonals:
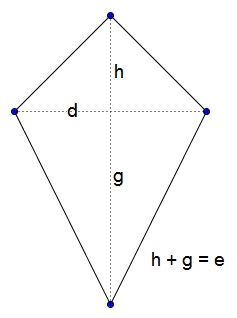
The same holds for a more general shape known as orthodiagonal quadrilateral, quadrilateral in which the diagonals are perpendicular to each other:
References
- J. Hadamard, Leçons de géométrie élémentaire, tome I, 13e édition, 1947, Editions Jacques Gabay, 1988, ISBN 2-87647-038-1.
- D. Hilbert, Foundations of Geometry, Open Court, 1999
- H. R. Jacobs, Geometry, 3rd edition, W. H. Freeman and Company, 2003
- Kiselev's Geometry. Book I. PLANIMETRY, adapted from Russian by Alexander Givental, Sumizdat, 2006.
- What Is Area
- Elementary Introduction into the Concept of Area
- Equidecomposition of a Triangle and a Rectangle: first variant
- Pick's Theorem
- Area of a Circle by Rabbi Abraham bar Hiyya Hanasi
- Area of a Circle by Leonardo da Vinci
- Volume and Area of Torricelli's Trumpet
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73580467
