So mathematicians sit around making patterns of ideas. What sort of patterns? What sort of ideas? Ideas about the rhinoceros? No, those we leave to the biologists. Ideas about language and culture? No, not usually. These things are all far too complicated for most mathematicians’ taste. If there is anything like a unifying aesthetic principle in mathematics, it is this: simple is beautiful. Mathematicians enjoy thinking about the simplest possible things, and the simplest possible things are imaginary. For example, if I’m in the mood to think about shapes - and I often am - I might imagine a triangle inside a rectangular box:

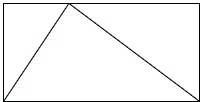
I wonder how much of the box the triangle takes up? Two-thirds maybe? The important thing to understand is that I’m not talking about this drawing of a triangle in a box. Nor am I talking about some metal triangle forming part of a girder system for a bridge. There’s no ulterior practical purpose here. I’m just playing. That’s what math is— wondering, playing, amusing yourself with your imagination. For one thing, the question of how much of the box the triangle takes up doesn’t even make any sense for real, physical objects. Even the most carefully made physical triangle is still a hopelessly complicated collection of jiggling atoms; it changes its size from one minute to the next. That is, unless you want to talk about some sort of approximate measurements. Well, that’s where the aesthetic comes in. That’s just not simple, and consequently it is an ugly question which depends on all sorts of real-world details. Let’s leave that to the scientists. The mathematical question is about an imaginary triangle inside an leave that to the scientists. The mathematical question is about an imaginary triangle inside an imaginary box. The edges are perfect because I want them to be— that is the sort of object I prefer to think about. This is a major theme in mathematics: things are what you want them to be. You have endless choices; there is no reality to get in your way.

On the other hand, once you have made your choices (for example I might choose to make my triangle symmetrical, or not) then your new creations do what they do, whether you like it or not. This is the amazing thing about making imaginary patterns: they talk back! The triangle takes up a certain amount of its box, and I don’t have any control over what that amount is. There is a number out there, maybe it’s two-thirds, maybe it isn’t, but I don’t get to say what it is. I have to find out what it is.

So we get to play and imagine whatever we want and make patterns and ask questions about them. But how do we answer these questions? It’s not at all like science. There’s no experiment I can do with test tubes and equipment and whatnot that will tell me the truth about a figment of my imagination. The only way to get at the truth about our imaginations is to use our imaginations, and that is hard work.

In the case of the triangle in its box, I do see something simple and pretty:

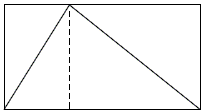
If I chop the rectangle into two pieces like this, I can see that each piece is cut diagonally in half by the sides of the triangle. So there is just as much space inside the triangle as outside. That means that the triangle must take up exactly half the box!

This is what a piece of mathematics looks and feels like.