Shredding the torus

We have considered several examples of cutting the torus along the lines parallel to the fundamental square of its plane model. Here I would like to discuss a more interesting problem where the cut is made along a slanted line. The problem of shredding a torus along such a line has two distinct solutions depending on whether the slope of the cut is rational or not.

First we'll look into the case of a rational slope which, perhaps surprisingly, under a general umbrella of the puzzles on graphs, is related to the Three Glass puzzle.

It's perhaps less surprising that the irrational case appears to be deeper, and the mathematics involved is less trivial. The case draws on a beautiful fact from the theory of rational approximation.

Rational Slope

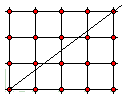
Thus, let's first assume the slope of a cut is a rational number r = p/q (3/4 on the diagram). Imagine the model square whose sides we identified to obtain a torus, embedded into a 2-dimensional integer grid (lattice). Previously, when the cut reached a side of the square we used identification of the opposite sides to skip to another side. Now, instead, let's continue the line beyond the square. Observe, that we can start the cut at the point (0,0). Indeed, if we proceed backwards from a torus to the square, we'll have to cut the torus along two perpendicular lines that will become the sides of the square. Therefore we may position the square any way we want.

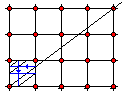
There are two ways to visualize the cut of the torus using its plane model. One, as before: continue the slanted line until it reaches one of the sides. Then follow the blue lines to the opposite side, and, 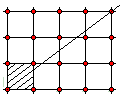from there, continue the line with the same slope, and so on. The second one is to cut the plane along the grid lines and stack the squares on top of each other. Assuming the plane transparent and looking from the top of the stuck, we'll see the resulting line segments inside a single square. Convince yourself that both ways lead to the same configuration of lines.

The fact that we deal with a rational slope implies that the line will pass through the node (q,p). This, in turn, implies that the line pattern inside the original square will be periodic. In other words, there will be just a finite number of line segments inside the square. Since the torus has two sides we are going to end up with a closed serpentine band that might be thought of as having been wrapped around the torus to start with.

Intuitively, the serpentine band is of constant width which means that the folds of the cut in the unit square are evenly spaced. Is it possible to prove this rigorously? How many of them are there?

Irrational Slope

If the slope of the cut is irrational, the shredding of the torus is more thorough by far. Theoretically speaking, the cut will never stop in the sense it will never pass through the same point twice. Furthermore, it will pass arbitrarily close to every point in the square (torus). Looking from above down at the stack of squares obtained by cutting the plane along the grid lines and piling the squares on top of each other, we'll see a blackened square (provided, of course, that it's the color used to depict the cut). The assertion is based on the following

Lemma

Let a and b be two numbers a,b∈[0, 1). Let r be an arbitrary irrational, i.e. r∈R-Q. Then

inf|b + m - r(a + n)| = 0,

where inf is taken over all possible pairs m,n of whole numbers.

Let me first show how this Lemma applies to the shredding of the torus. Let (a, b) be a point inside the model unit square. As in the rational case, assume the cut with an irrational slope r starts at the origin (0, 0). Translate the point (a, b) integer units left, right, up, and down so that the points (a + n, b + m) will appear in every small square of the grid. (When squares are stacked on top of each other, all such points project onto one single point, viz. (a, b).) From Lemma it follows that the vertical distance from the line y = rx to the set of these points is 0. Piling squares on top of each other, we see that (folds of) the cut will pass arbitrarily close to the point (a, b).

Proof of Lemma

I am going to apply the Pigeonhole Principle to show that for any integer Q, there exists a pair m,n such that |b + m - r(a + n)| < 1/Q. The difference on the left side of the inequality may be assumed to never vanish. Indeed, since the set of rational pairs is dense in R², we may assume that both a and b are rational so that the difference will be irrational, thus never 0, for all values of m and n.

Consider {0}, {r}, {2r}, ..., and so on, where {A} is the fractional part of A: {A} = A - floor(A). If we take more than Q terms, then, by the Pigeonhole Principle, there exist two numbers n and d such that 0 < {r(n+d)} - {rn} < 1/Q. Note that d might be negative. (The cut is completely defined by its slope. However, the direction of the cut along this slope is arbitrary. We might cut one way or another or both if we so wish. Negative d corresponds to the motion in the direction opposite to the originally selected.)

At this point it's useful to invoke geometric intuition. Imagine a circle with the circumference equal to 1. Imagine an infinite tape with distance r between the ticks. Start wrapping the tape around the circle and watch the locations of the ticks. The inequality 0 < {r(n+d)} - {rn} < 1/Q means that ticks n and (n+d) fall within the distance 1/Q of each other. But then the same will be true for the ticks (n+d) and (n+2d), and also for the pair (n+2d) and (n+3d), and so on. Every d^th tick (starting with the n^th) falls on the circle at a fixed distance (which is less than 1/Q) from the previous one. Thus, starting with the n^th tick, we measure intervals of fixed length (less than 1/Q) over the circle. Clearly, every point on the circle will eventually fall inside one of those intervals, and thus be at the distance less than 1/Q from one of such ticks, or, unfolding the circle back into the unit interval, from one of the numbers {r(n+kd)} (or {r(n+kd)}±1) for some integer k.

Of course, we might have placed the beginning of the tape at point a instead of 0, in which case, every point in the unit interval would be located within distance 1/Q from one of the points {r(a+n+kd)} or {r(a+n+kd)}±1. In particular, this is true of b, which proves the Lemma.

Reference

R.J.Wilson, Graphs And Their Uses, MAA, New Math Library, 1990.

49552066