Inscribing a regular pentagon in a circle - and proving itScott E. BrodieConstructions by straight-edge and compass of several regular polygons - the equilateral triangle, square, hexagon, and octagon, are familiar. Indeed, the construction of an equilateral triangle is the very first proposition in Euclid's Elements (I.1). Less well known is the surprisingly simple construction of a regular pentagon by the same methods. The construction and its verification give another illustration of how the Pythagorean Theorem is woven into the structure of geometry, even though there are no right angles in a pentagon. (A regular pentagon can also be modeled by flattening an overhand knot tied from a strip of uniform width.) 
Start with a circle of radius 1 (Figure 1). Construct perpendicular diameters AB and CD. Bisect the radius OB at M. With center M and radius MC, draw an arc intersecting radius OA at N. I claim that CN is the side of the regular pentagon inscribed in the circle. To verify the construction, look first at the "star pentagram", a regular pentagon containing a five-pointed star inscribed within it (Figure 2). Consider the two diagonals radiating from a single vertex. These two diagonals enclose one side of the pentagon, forming an isosceles triangle (such as CPQ in Figure 2). 
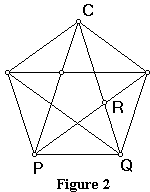
The Greek geometers realized that this triangle demonstrates a property of "self-similarity" comparable to that of the better-known "golden rectangle": since the ray PR bisects angle CPQ, triangle PQR is similar to the original triangle CPQ. Thus Now return to the original construction (Figure 1). To compute the length of segment CN, use the Pythagorean Theorem twice: On the other hand, let s be the length of the side of the inscribed pentagon, d the length of a diagonal, and t the length of the segment DQ in the figure (the side of a regular decagon inscribed in the same circle). We have But triangle ODQ is similar to triangle CPQ, so we have likewise 1 = φt. So far, we have two equations in the three variables d, s, and t. Fortunately, the Pythagorean Theorem gives us a third equation: triangle CDQ is inscribed in a semicircle, so angle DQC is right, and Then s = d / φ = φ-1√4 - 1/φ² = √5/2 - √5/2, QED. Elegant as this construction is, this is not how it appears in Euclid's Elements. The construction is commonly attributed to another Greek mathematican Ptolemy who lived some 400 years later. Euclid's procedure (IV.11) is as follows: begin with a line segment divided by a point into two segments whose ratio is φ (II.11). (Note how this construction bears a strong resemblance to the construction of the pentagon given above.) Next, construct an isosceles triangle with sides proportional to φ, φ, and 1 (IV.10). Euclid notes that in such a triangle, the base angles are double the vertex angle. Inscribe a triangle similar to this one in a given circle (IV.2) . Now bisect the base angles of the inscribed triangle. The intersections of the bisecting rays with the circle, together with the vertices of the inscribed triangle, determine the desired pentagon. (This construction is easily Regular Pentagon Inscribed in Circle by Paper Foldingimplementable by paper folding. Also, there is also an elegant 19th century Japanese construction of the regular pentagon.) 
Fibonacci Numbers
Golden Ratio
|Contact| |Front page| |Contents| |Geometry| |Up| |Store| Copyright © 1996-2012 Alexander Bogomolny |
| 41173604 |
