Mascheroni Construction of a Regular Pentagon

In 2002 we have given a simple 5-step compass-only (Mascheroni) construction of the golden section. Here we note that with two additional circles, it is possible to construct the vertices of a regular pentagon. As usual, we denote by P(Q) the circle with center P and passing through Q.

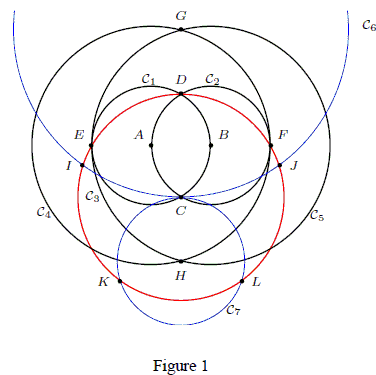
Construction 1. Given two points A and B,

1. C₁ = A(B),
2. C₂ = B(A) to intersect C₁ at C and D,
3. C₃ = C(D) to intersect C₁ at E and C₂ at F,
4. C₄ = A(F),
5. C₅ = B(E) to intersect C₄ at G and H.
6. C₆ = G(C) to intersect C₃ at I and J,
7. C₇ = H(C) to intersect C₃ at K and L.

Then DIKLJ is a regular pentagon.

Proof: In a 2002 paper, we have shown that the first five steps above lead to four collinear points C, D, G, H such that D divides CG, and C divides DH, in the golden section.

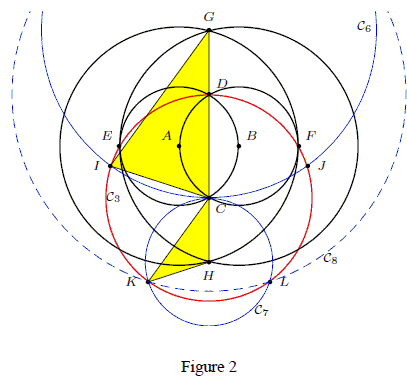
1. This means that in the isosceles triangle GCI, GC/IC = GC/DC = φ. The base angles are 72° Therefore, ∠DCI = 72° By symmetry, ∠DCJ = 72°.

2. Also, in the isosceles triangle HCK, KC/CH = DC/CH = φ. The base angles are ∠36°. It follows that ∠KCH = 36° By symmetry, ∠LCH = 36°, and ∠KCL = 72°.

3. Since C is on the line GH, ∠ICK = 180° - ∠GCI - &anf;KCH = 72°. By symmetry, ∠JCL = 72°.

   Therefore, the five points D, I, K, L, J are equally spaced on the circle C₃.

   They form the vertices of a regular pentagon.

Remark. The circle C₇ can be replaced by C₈ with center D and radius IJ. This intersects C₃ at the same points K and L.