Regular Pentagon Construction by Y. Hirano

Pentagon being the next in line regular polygon after ubiquitous equilateral triangles and squares, many ways have been discovered to construct it with straight edge and compass, see for example S. Broddie's article. In a follow-up to a sangaku concerned with regular pentagon measurements, [Fukagawa & Pedoe, pp. 133-134] give an elegant Euclidean construction of a regular pentagon due to Yosifusa Hirano, probably a 19^th century math fan. The construction has been included in a manuscript Sanpo Jyojutu Kaigi, meaning Solutions to Sanpo Jyojutu, by Chorin Kawakita (1840-1919). Kawakita wrote: "Hirano, my friend, discovered the method of construction of regular pentagon. This method is original, elementary and excellent. So, I am writing this method here."

Hirano's construction is illustrated by the following diagram:

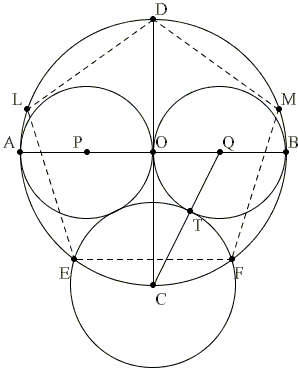
In the diagram, AB and CD are perpendicular diameters of a circle with center O. Circles (P) and (Q) have diameters AO and BO, respectively. Line CQ intersects (Q) in T. Circle C(T) has center C and radius CT and intersects the given circle in E and F which are two successive vertices of a regular pentagon inscribed in the circle (O). Indeed, assuming the radius of (O) is 1,

CQ = √1 + (1/2)² = √5 / 2.

By construction,

CE = CF = √5 / 2 - 1/2 = (√5 - 1)/ 2.

Further,

sin(∠CDF) = CF / CD = (√5 - 1)/ 4,

which, as we know, means that ∠CDF = 18°. Thus, ∠COF = 36° and ∠EOF = 72°, as needed.

References

H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

Write to:

Charles Babbage Research Center
P.O. Box 272, St. Norbert Postal Station
Winnipeg, MB
Canada R3V 1L6

Approximate Construction of Regular Pentagon by A. Durer
Construction of Regular Pentagon by H. W. Richmond
Inscribing a regular pentagon in a circle - and proving it
Regular Pentagon Construction by Y. Hirano
Regular Pentagon Inscribed in Circle by Paper
Mascheroni Construction of a Regular Pentagon

40619408