True Calculus Proof of the Pythagorean Theorem
John Molokach whose first proof of the Pythagorean theorem based on Calculus contained flaws and was roundly criticized, has produced a version that appears to avoid circular reasoning.
John Molokach
December 20, 2010
Consider a right triangle with legs of length a and b and hypotenuse of length c. Construct a rectangular coordinate system so that the vertices of the triangle have coordinates (0, 0), (a, 0), and (a, b). Draw the semicircle in the upper half-plane centered at the origin with radius c. This semicircle passes through the points (a, b) and (0, c).
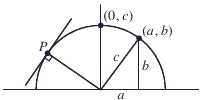
Euclid showed in Book III, Proposition 16 that if P is any point on the semicircle, then the line through P that is perpendicular to the radius from the origin to P is tangent to the semicircle, in the sense that it does not intersect the semicircle at any point other than P. We leave it as an exercise for the reader to verify that this line also satisfies the calculus definition of the tangent line to the semicircle at P. It follows that the semicircle must be the graph of a solution to the differential equation
This proof warrants a few comments. Note that, compared to the first attempt, John omits the word "distance". While it is possible to define the circle as the locus of points on a fixed distance from a center, this definition is rather misleading because we have been conditioned to treat the distance between two points in the plane using the Pythagorean identity. As a matter of fact, however, Euclid has developed the whole of his geometry without recourse to this concept. Geometry, even the planar one, only needs the concept of length of a straight line segment and the assumption that this length could be measured regardless of how the segment is placed on the plane.
Calculus of a single variable, too, does not need nor any of its definitions use, the two-dimensional distance.
The basic notions of analytic geometry - the coordinate system, the linear equations of a straight line, the slope - can be introduced without the Pythagorean theorem.
The fact that the product of the slopes of two perpendicular lines equals -1 follows from the fact that the angles in a triangle add up to 180°, i.e., the Parallel postulate.
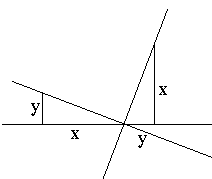
This is all that is necessary for John's proof. An objection that was raised on several occasions that the Pythagorean theorem is equivalent to the Parallel postulate, is rather irrelevant. The concept of similarity is only viable in Euclidean geometry and indeed is being used by practically any proof of the Pythagorean theorem. John's proof does neither more nor less.
- Pythagorean Identity and ODEs
- The Pythagorean Theorem from a Combinatorial Identity
- Derivative of Sine and Cosine
- Taylor Series Approximation to Cosine
- True Calculus Proof of the Pythagorean Theorem
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71532090
