Calculus Proof of the Pythagorean Theorem

This proof has been posted by John Molokach.

Begin with a right triangle drawn in the first quadrant. The legs are variables x and y and the hypotenuse is a fixed positive value c, where the vertex of the angle whose sides contain x and c is the origin.

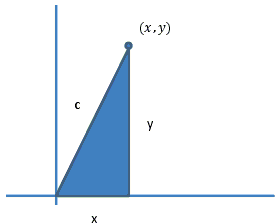
The slope of the line containing c is m = y/x.

and the line perpendicular to the line containing c at (x, y) is m = -x/y.

Now consider the set of all points (x, y) that are a fixed distance c from the origin where y > 0.

All possible points (x, y) in this scenario will lie on the solution curve to dy/dx = -x/y.

Finding a general solution to the differential equation dy/dx = -x/y we have

Now using an initial condition (x, y) = (c, 0) we have:

So we have the particular solution x² + y² = c². Pick arbitrary values for (x, y) on the curve in the first quadrant, call them (a, b) and you have a² + b² = c². Q.E.D.

Critique

Before looking for faults, let me shorten the proof.

First of all, starting with a triangle (x, y, c) and stating that lines with slopes y/x and - x/y are perpendicular had no effect on the proof. The opening paragraph, the picture and the two following sentences are unnecessary and may be setting the wrong kind of anticipation. That they have becomes apparent from the next sentence.

We are going to write, then solve a differential equation and see what comes out. Until we have done that, "the set of all points at a fixed distance c from the origin" appears to drop out of the blue and is, again, not used in the proof, but to mislead.

What remains? For every point (x, y) in the plane, define a direction with the slope -x/y. This is called a vector field. Solutions to the equation we are setting up will be the integral curves of that field, i.e., curves whose tangents at every point have the slopes define by the vector field, -x/y, in this case.

We solve the equation and find that the general form of the solution is x² + y² = E. Does a solution cross the x-axis. To find out, we set y = 0 and reduce the equation of the curve to x² = E. If E is positive, we can define c, with c² = E, so that the solution for a particular E crosses the x-axis at (c, 0). Points on the curve do satisfy the equation x² + y² = c². There is no denying it. But then what?

Unless the distance d(x, y) from the origin to point (x, y) has been defined up front via the Pythagorean identity

There is nothing that can be said as to the meaning of the equation x² + y² = c². For example, the distance d(x, y) might have been defined differently as

The fact that a differential equation led to curves x² + y² = c² may suggest that defining the distance via the Pythagorean identity and not anyhow else may be a very sensible idea, but this is a far cry from proving the theorem.

Important Note

Some time later John has submitted a corrected version of the proof that appears to avoid the pitfalls of circular reasoning.

|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|