Ptolemy's Theorem

Manifesto | Amazon store | Term index | What changed? | rss feed

Ptolemy's Theorem

Let a convex quadrilateral ABCD be inscribed in a circle. Then the sum of the products of the two pairs of opposite sides equals the product of its two diagonals. In other words,

AD·BC + AB·CD = AC·BD

Remark

Ptolemy of Alexandria (~100-168) gave the name to the Ptolemy's Planetary theory which he described in his treatise Almagest. The book is mostly devoted to astronomy and trigonometry where, among many other things, he also gives the approximate value of π as 377/120 and proves the theorem that now bears his name. The name Almagest is actually a corruption of the Arabic rendition "Al Magiste" - The Greatest - of the Greek H Megisth Suntaxiz (E Megiste Syntaxis).

This classical theorem has been proved many times over. Following is the simplest proof I am aware of. (There is another simple proof of a recent vintage.)

Proof

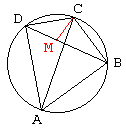
On the diagonal BD locate a point M such that angles ACB and MCD be equal. Since angles BAC and BDC subtend the same arc, they are equal. Therefore, triangles ABC and DMC are similar. Thus we get CD/MD = AC/AB, or AB·CD = AC·MD.

Now, angles BCM and ACD are also equal; so triangles BCM and ACD are similar which leads to BC/BM = AC/AD, or BC·AD = AC·BM. Summing up the two identities we obtain

AB·CD + BC·AD = AC·MD + AC·BM = AC·BD

Remark

Ptolemy's theorem admits a useful generalization: for four points A, B, C, D, not necessarily concyclic,

AB·CD + BC·AD ≥ AC·BD

which is known as Ptolemy's inequality.

The following problem is discussed in Honsberger, Mathematical Morsels, p172:

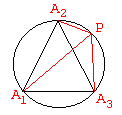
Let A₁A₂A₃ denote an equilateral triangle inscribed in a circle. For any point P on the circle, show that the two shorter segments among PA₁, PA₂, PA₃ add up to the third one.

Solution

Let s denote the length of the side of the given triangle. By Ptolemey's Theorem we have

s·PA₁ = s·PA₂ + s·PA₃

Therefore,

PA₁ = PA₂ + PA₃

Remark

This result has an interesting generalization to the case of a regular 3n-gon inscribed in a circle: Of the 3n chords obtained by connecting a point P with vertices of the polygon, the sum of the 2n shortest ones equals the sum of the n longest.

The problem itself is sometimes attributed to Van Schooten (1615 � 1660), see, for example, The Changing Shape of Geometry, (C. Pritchard, Cambridge University Press, 2003), p. 184, where two additional proofs could be found.

Remark

Ptolemy's theorem is a powerful result. With its help we establish the Pythagorean Theorem. Combined with the Law of Sines, Ptolemy's theorem serves to prove the addition and subtraction formulas for the sine function. It has a short proof in complex numbers. The following generalization is sometimes attributed to the great 9^th century Indian mathematician Mahavira (or Mahaviracharya, meaning Mahavira the Teacher).

In a cyclic quadrilateral ABCD, let a, b, c, d denote the lengths of sides AB, BC, CD, DA, and m, n the lengths of the diagonals BD and BC. Then Mahavira's result is expressed as

m² = (ab + cd)(ac + bd)/(ad + bc) and
n² = (ac + bd)(ad + bc)/(ab + cd)

H. Eves gives a proof as a sequence of exercises in [Great Moments in Mathematics Before 1650, p. 108]:

Let t be the diameter of the circmcircle of ABCD and θ the angle between either diagonal and the perpendicular upon the other.

Then, (using triangle's formula ab = 2hR applied to DAB and DCB), we get

mt·cosθ = ab + cd and
nt·cosθ = ad + bc

So m / n = (ab + cd) / (ad + bc) which is called Ptolemy's second theorem.

Also mn = ac + bd (Ptolemy relation)

Multiplying those last 2 equations, we get:

m² = (ab + cd)(ac + bd) / (ad + bc)

Dividing instead, we get:

n² = (ac + bd)(ad + bc) / (ab + cd).

Finally, we also get