What is a number?

To paraphrase Albert Einstein, a number in and by itself has no significance and only deserves the designation of number by virtue of its being a member of a group of objects with some shared characteristics. The most common characteristic of numbers is that they can be added and multiplied to produce other numbers in their group. However, not all objects that can be added or multiplied are designated as numbers.

As a matter of fact, there are many different kinds of numbers.

• rational and irrational
• real and complex
• imaginary
• algebraic and transcendental
• perfect
• surreal
• hyperreal numbers
• square and triangular numbers

Let's talk a little about each of these in turn.

Rational and Irrational numbers

A number r is rational if it can be written as a fraction r = p/q where both p and q are integers. In reality every number can be written in many different ways. To be rational a number ought to have at least one fractional representation. For example, the number

((√5 + 1)/2)² + ((√5 - 1)/2)²

may not at first look rational but it simplifies to 3 which is 3 = 3/1 a rational fraction. On the other hand, the number √5 by itself is not rational and is called irrational. This is by no means a definition of irrational numbers. In Mathematics, it's not quite true that what is not rational is irrational. Irrationality is a term reserved for a very special kind of numbers. However, there are numbers which are neither rational or irrational (for example, infinitesimal numbers are neither rational nor irrational). Much of the scope of the theory of rational numbers is covered by Arithmetic. A major part belongs to Algebra. The theory of irrational numbers belongs to Calculus.

Using only arithmetic methods it's easy to prove that the number √5 is not rational. Just to remind, √5 stands for the number whose square equals 5. Thus Arithmetic can show that, when squared, no rational number gives 5. It's impossible to derive in Arithmetic that such a number actually exists.

Proof that for no rational number r = p/q, (p/q)² = 5

Assume that a rational number r exists such that r² = 5. In the representation r = p/q assume p and q are mutually prime, i.e. have no common divisors. The fraction p/q in this case is called irreducible. It would be a very legitimate question to ask whether every rational number has an irreducible representation. See if you know enough to answer this question.

Thus 5q² = p² so that p² is divisible by 5. 5 is a prime number (it has no other divisors but itself and 1). Therefore I can use a theorem by Euclid (Elements, VII.30) (see also Ref [2]) to claim that since 5 is a factor of p² it also divides p, i.e. p = 5s. Substituting this into 5q² = p² and dividing by 5 gives q² = 5s². By the same token, q is then divisible by 5 which makes the fraction p/q reducible. Contradiction.

(In fact for any integer n, which is not a square of another integer, √n is irrational. The above proof is commonly used to prove the irrationality of √2. This is because √2, being the length of the diagonal in a unit square, was the first number proved not to be rational. There is in fact great many ways to establish this result with various degrees of intuitive appeal.)

Intuitively the number √5 should exist. Indeed, apply the Pythagorean Theorem to the right-angled triangle with sides 1 and 2. Then (hypotenuse)² = 1² + 2² = 5. Thus there exists a line segment whose length should be equal √5. For, otherwise, what else might it be equal to? As I already mentioned, it takes methods beyond Arithmetic to introduce irrational numbers. It is interesting to observe the characteristic unity of Mathematics as reflected in this example. In Arithmetic we pose and successfully solve a variety of problems until we unwittingly ask to solve a very innocently looking equation x² = 5. However, Arithmetic proves powerless to solve the equation. Geometry suggests that a solution should exists. Calculus actually solves the problem.

As often the case in Mathematics, there are many ways to define irrational numbers. We'll use the one suggested by Georg Cantor (1845-1918), the father of modern Set Theory. Incidentally, Cantor's doctoral thesis was titled "In mathematics the art of asking questions is more valuable than solving problems." (see Ref [4])

Without giving a rigorous definition let me say that Cantor defined irrational numbers as limits of convergent sequences of rational numbers (see Ref [1]). The idea is quite intuitive. For simplicity, I'll handle only numbers between 0 and 1. Start with writing rational numbers as decimal fractions 1/5 = 0.2, 3/8 = 0.375, 1/3 = 0.333..., 1/7 = 0.142857. As you see, some rational numbers are written as finite decimal fractions (1/5 and 3/8). To write others will take an infinite sequence of digits. That's why we write ellipses in the decimal expansion of 1/3. The more 3s you write the closer the decimal fraction comes to 1/3 but no finite expansion will ever equal 1/3 exactly. In case of 1/7 brackets designate a period. In other words, the decimal expansion of 1/7 = 0.142857142857142857142857... - the period 142857 is repeated indefinitely. The expansion of 1/7 also requires an infinite sequence of digits. In the math parlance 1/7 is the limit of a convergent sequence

a₁ = 0.1, a₂ = 0.14, a₃ = 0.142, ...

The sequence converges because |1/7 - a_n| < 10^-n which only states an obvious fact that any fraction 0.... that starts with n 0s ought to be less than the fraction that has 1 in the nth position. But this is true for an arbitrary sequence of digits, not necessarily periodic. Thus Cantor studied such decimal expansions and observed that periodic expansions correspond to rational numbers whereas the non-periodic ones correspond (by his definition) to the irrational numbers. Please note that every sequence of digits corresponds to a convergent sequence of rational numbers and, therefore, represents a number, rational or irrational. (We'll talk of positive numbers. Any sequence of digits is represented by a nondecreasing sequence of rational number. The decimal portions of such sequences are bounded by one of the terms in the sequence .9, .99, .999, ... Therefore, the decimal portions have a limit bounded by .999... = 1.)

Lemma 1

Corollary

In all four statements assertion of existence of a single number can be replaced with the assertion of existence of infinitely many numbers.

Proof of Lemma 1

1. a < (a + b)/2 < b and (a + b)/2 is rational.

2. Let decimal expansions of two irrational numbers a and b (a < b) first differ in the n^th digit. Consider the number b_n obtained from b by cutting all the digits after the n^th. Then a < b_n < b. Of course, being a finite decimal expansion, b_n is a rational number.

3. Let the decimal expansions of two rational numbers a and b (a < b) first differ in the n^th digit. Then, as before, consider b_n: a < b_n < b. Assume b has non-zero digits after the n^th. Think of how to amend the proof if it does not. Let b_m be the first non-zero digit of b after b_n. Append to b_n m - n zeros and then any random sequence of digits. Every time you append a digit you obtain a new rational number between a and b. The sequence is convergent to a limit between a and b. If you make an effort to avoid periodic sequences the limit will be irrational.

   Will Rose suggested a different way of growing b_n into an irrational number. Pick any number r known to be irrational. It could be the square root of 2, e, π or any other irrational number. Since the product of two rational numbers is rational, r·10^M is bound to be irrational for any integer M. Take N so large as to make r·10^-N smaller than b_m10^-m. Then use the digits of this number in lieu of the random selections as above.

   (An Aside: Is number 1234567891011121314151617181920212223... periodic?).

4. The proof is a variation on the above.

Collectively, rational and irrational numbers are called real. Thus a real number is either rational or irrational. (In passing, Ian Stewart questions the wisdom of calling irrational numbers real: How can things be real if you can't even write them down fully?) From Lemma 1 it may appear that rational and irrational numbers play symmetric roles in the set of real numbers. One of the many Cantor's contributions was in showing that there are various kinds of infinities. While it is true that there are infinitely many rational numbers and infinitely many irrational numbers, in a well defined sense, the are more irrational numbers than rational.

Cantor began with the notion that counting or enumeration of objects brings finite sets into a 1-1 correspondence with finite segments of the set of integers. When you say you have two hands you mean that it's possible to assign the number 1 to one hand and the number 2 to another and no hands will be left uncounted. Right? Is it what you mean? Cantor applied the notion of the 1-1 correspondence to infinite sets such as the sets of integers, rational, irrational or real numbers.

With the notion of the 1-1 correspondence came quite a few surprises. (Actually the fact that handling infinities is wrought with surprises was already known to medieval thinkers, see Ref [3]. Check also Hilbert's paradox of the Grand Hotel.) For example, the sets of odd numbers, even numbers, complete squares or cubes, the set of integers greater than 1996 all can be brought into a 1-1 correspondence with the set of all integers (of which they are subsets.) Indeed, the following table summarizes how it's done.

Integers	Odd numbers	Even numbers	Squares	Cubes	Greater than 1996
n	2n-1	2n	n2	n3	n+1996
1	1	2	1	1	1997
2	3	4	4	8	1998
3	5	6	9	27	1999
4	7	8	16	64	2000
...	...	...	...	...	...

Let N, E, and O denote the sets of all counting numbers, all even and all odd numbers, respectively. Then, on the one hand, N~E and N~O (where tilde signifies existence of a 1-1 correspondence). On the other hand, N~N = E+O. To many it may look like 1 = 2. But we can also adopt a more positive attitude.

I'll call two sets A and B equivalent if A~B. What we discovered was that infinite sets may be (and in fact are) equivalent to their own subsets and that the union of two equivalent (infinite) subsets is equivalent to either of them. Actually we may have gained an insight into the fundamental differences between finite and infinite sets. No finite set is equivalent to a proper subset of its own whereas every infinite is. This is known as the Dedekind's Theorem, but is often taken as a definition of infinite sets.

A set A is called countable (or enumerable, or denumerable, and, sometimes, even numerable) if A~N, i.e. if it's equivalent to the set of all integers. Our second discovery can be formulated as

Lemma 2

Union of two countable sets is countable.

Proof of Lemma 2

Let us denote the two sets A and B. We are given that A ~ N and B ~ N. Since N ~ E and N ~ O we get A ~ E and B ~ O. Therefore A + B ~ E + O = N.

It follows from Lemma 2 but also can be proven directly that the union of a finite number of countable sets is countable. A more exciting fact is given by

Lemma 3

Union of a countable number of countable sets is countable.

Proof of Lemma 3

For a proof please refer to a separate page.

Corollary

A Cartesian product of two countable sets is countable. (Cartesian product of two sets A and B consists of pairs (a, b) where a ∈ A (a is element of A) and b ∈ B.)

Cantor's Set Theory is a fascinating topic in its own right but what was the purpose of swaying away from the discussion of various sets of numbers? Besides being useful in the forthcoming discussion on algebraic and transcendental numbers, there was a more immediate goal.

Lemma 4

The set Q of all rational numbers is equivalent to the set N of all integers.

Proof of Lemma 4

It's a direct consequence of Lemma 3. To get an enumeration of Q, write in the diagram above 1/1 instead of 11, 1/2 instead of 12 and so on. Put another way, the function F(m/n) = (m + n - 1)(m + n - 2)/2 + m enumerates all possible representations of positive rational numbers. But every rational number has infinitely many fractional representations. Therefore, Q is at most countable. It's clearly infinite. Proving that it's indeed countable takes a little more perseverance and I prefer to refer to Ref [5].

Another appealing proof can be found on a separate page. And a third one is based on enumeration of fractions on the Stern-Brocot tree.

Lemma 5

The set Q of all rational numbers is equivalent to the set N of all integers. The set I of all irrational numbers is not countable.

Proof of Lemma 5

The proof is a variant of what is known as the diagonal argument. Again I shall only consider numbers between 0 and 1. Irrational numbers have been defined as decimal (non-periodic) fractions. Assume it is possible to enumerate all such decimals. Let choose an enumeration and list the decimals in the corresponding order:

a₁ = 0.a₁₁a₁₂a₁₃a₁₄...
a₂ = 0.a₂₁a₂₂a₂₃a₂₄...
a₃ = 0.a₃₁a₃₂a₃₃a₃₄...
...

where a_mn stands for the n^th digit of the m^th decimal. The approach I employ is Cantor's famous diagonal process. To remind, we made an assumption that all the decimals between 0 and 1 have been listed in the sequence above. I'll get a contradiction by showing that at least one decimal is missing from the list. The decimal b = 0.b₁b₂... is constructed a digit by digit. Select b₁ to be any digit but a₁₁. Select b₂ to be any digit but a₂₂. And in general, select b_n to be any digit but a_nn. Then b can't equal any decimal a_n, n = 1, 2, 3, ... because b differs from a₁ in the first digit; it differs from a₂ in the second digit and so on.

(An absolutely delightful argument of a recent vintage the does not refer to the diagonal process is well worth looking into.)

From Lemma 1 it appeared that the distributions of rational and irrational numbers have much in common. Between any two numbers of one kind there always existed numbers of the same and of the other kind. However, rational numbers form a countable set whereas irrational form a set which is not countable.

To conclude the discussion of rational and irrational numbers:

• There are infinite sets for which no 1-1 correspondence exists. There are various kinds of infinite sets. This topic belongs to the realm of the Set Theory and, more particularly, to the Theory of Transfinite Numbers (Cardinals).
• The property expressed in Lemma 1 is known as density of both rational and irrational numbers on the straight line and, as such, belongs to the General Topology. Sets could be dense without being equivalent.
• Expectations based on experience with finite sets should not be extrapolated to the sets infinite.

Algebraic and Transcendental numbers

Now let us consider polynomial equations with integer coefficients:

P_n(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀ = 0

Real roots of such equations are said to be algebraic. In other words, a number a is called algebraic if it satisfies an algebraic equation: P_n(a)=0 for some polynomial P_n(x) with integer coefficients. Rational numbers and integers are all algebraic. Indeed, for a given rational number r = p/q take n = 1 and P₁(x) = qx - p. Obviously P₁(r) = 0. √5 is also algebraic for it solves the equation P₂(x) = x² - 5 = 0.

If a_n ≠ 0 then the polynomial is said to be of order n.

Polynomials of order 1 have two integer coefficients each, a₁ and a₀. It follows from Lemma 3 that the set of all polynomials of order 1 is countable. Directly or by induction, one can prove a general assertion. For every n the set of polynomials of order n is countable. The Fundamental Theorem of Algebra claims that a polynomial of order n has exactly n (perhaps complex) roots. Thus the set of all numbers that satisfy some equation of order n is countable. The subset of this set that consists of real numbers is as well countable. Applying once more Lemma 3 we get

Lemma 6

The set of all algebraic numbers is countable.

Real numbers that are not algebraic are called transcendental. Thus the set R of all real numbers is the union of two sets - algebraic and transcendental. The set R is not countable while there are countably many algebraic numbers. Therefore the set of all transcendental numbers is not countable either. Given the difficulty of establishing whether a given number is algebraic or not, this was one of Cantor's early surprising results.

It's known that π and e are transcendental. e was proven to be transcendental by Hermite in 1873, and π by Lindemann in 1882. e^π is transcendental from the Gelfond's Theorem. At least one of πe and π + e is transcendental. It is not known if e^e, π^π or π^e are transcendental.

A note

Note that although most of the real numbers are transcendental (since there is only countably many algebraic numbers), transcendentality is proven a number at a time.

Real and Complex numbers

The union of rational and irrational numbers forms the set of real numbers. Complex numbers are pairs c = (x, y) of two real numbers. Since the situations of having to handle two numbers instead of one is more complex than handling a single number, the terminology is well justified. An impetus for developing the theory of complex numbers came originally from unsolvability of a simple equation x² + 1 = 0 in the set of real numbers. In the set of complex numbers the equation has two solutions ±i. The rest of the complex numbers could also be defined by adding this new number i to the set of reals and postulating that usual arithmetic operations (addition, subtraction, multiplication) apply to the expanded set and all the laws known to hold for these operations hold for the new set as well. Such an action is known as the closure with respect to the given algebraic operations. This is very satisfactory that without breaking existing laws and by adding a single new number we actually get a set of numbers in which every polynomial equation with real coefficients has a solution. This is known as the Fundamental Theorem of Algebra. Moreover, the theorem also holds for every polynomial with complex coefficients.

Complex numbers have unusual properties especially when it comes to differentiation. With real numbers differentiation is a starting point of Calculus and Real Analysis. With complex numbers it leads to the Analytic Function Theory.

Imaginary numbers

As was just defined, a complex number c is a pair (x, y) of two real numbers. x in the pair is called the real part and y is the imaginary part of the complex number c. This notion of imaginary part is rather unfortunate for the following reason.

Complex number (x, y) is associated with a point (x, y) in the standard coordinate system in the plane. Points (x, 0) lie on a very real X-axis whereas points (0, y) lie on a no less real Y-axis. When it's desirable to emphasize the algebraic nature of complex numbers it's customary to write (x, y) = x + iy thus making distinction between the real part x and the imaginary part y more palpable. However, there are situations where the word "imaginary" furnishes the most suitable Description of the circumstances.

In the plane the distance between two points c₁ = (x₁, y₁) and c₂ = (x₂, y₂) is defined as dist(c₁, c₂)² = (x₁ - x₂)² + (y₁ - y₂)². Which is quite natural due to the Pythagorean Theorem. Then the circle with radius r and center at c₀ = (x₀, y₀) consists of all points c = (x, y) such that dist(c, c₀) = r. In other words,

(1)	(x - x0)2 + (y - y0)2 = r2.

This is an equation of a real (i.e. one that could be drawn with a compass) circle in a real (although consisting of complex numbers) plane. Now, mathematicians did not stop at a simple equation x² = 1 but were curious enough to take matters further by changing the sign on the right-hand side. The new equation x² = -1 turned out to be the source of much of the discoveries in the last two hundred fifty years. Continuing in their usual manner, mathematician did not stop at changing signs at the equation (1) either. Since, i² = -1, they got

(2)	(x - x0)2 + (y - y0)2 = (ir)2.

which is really an imaginary circle with a real center c₀ but an imaginary radius ir. Getting this far, it must be said that the polynomial equation (2) has no real solutions (x, y) or, which is the same, no complex solutions c. However, if, for simplicity's sake, we consider a circle centered at the origin

(3)	x2 + y2 = (ir)2

then it'll become obvious that equations (2) and (3) do have solutions. For example, the pair (0, ir) solves (3). This should probably be called a really imaginary number (see Ref [7]).

Perfect numbers

Every number n is divisible by at least 1 and n. The sum of all divisors of n is called s(n). If n = p^aq^b..., where p, q ... are all primes, then s(n) = (1+ p + ... + p^a)(1 + q + ... q^b)... . n is perfect if it equals the sum of its divisors including 1 but excluding n. In other words, n is perfect if s(n) = 2n.

The numbers for which s(n) < 2n are known as deficient. For example, s(8) = 1 + 2 + 4 + 8 = 15 and s(15) = 1 + 3 + 5 + 15 = 24, so that 8 and 15 are deficient. The numbers for which s(n) > 2n are called abundant. 12 is such a number, because s(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28 > 2·12.

Euclid in his Elements, IX.36 proved that if, for a prime p, p+1 = 2^k, then 2^k-1p is perfect. Leonhard Euler (1707-1783) in a paper published posthumously, showed that every even perfect number has Euclidean form. Euler was absolutely blind for the last 18 years of his life. So it's likely this result was among those obtained by already blind Euler.

The first perfect number is 6 (= 1 + 2 + 3). 28 (= 1 + 2 + 4 + 7 + 14) is the second. Then come 496 and 8128. The fifth perfect number 33550336 has been calculated by Hudalrichus Regius (1536), not 500 hundred years ago.

Surreal numbers

Surreal numbers have been invented by John Conway who, among many other things, created the famous Game of Life. Donald Knuth's brochure Surreal Numbers gives a very popular but rigorous introduction into the development of surreal numbers successively starting with literally nothing. This is the only aspect of the theory that I intend to mention here.

A surreal number (see a short introduction or in relations to games) is a pair of sets {X_L, X_R} where indices indicate the relative position (left and right) of the sets in the pair. The first number to be constructed is 0 = {,} for which both left and right sets are empty. The rest of surreal numbers (included are the numbers we discussed so far and myriads of numbers some of which I have a difficulty imagining) are formed starting with 0 and applying just two simple rules. Truly, it's a creation of something from nothing.

Martin Gardner (Ref [9]) describes application of surreal numbers to the theory of games also developed by John Conway.

Square and Triangular numbers

Every one knows how to compute a square of a given number especially if it's not too large. 2² = 4, 3² = 9, 4² = 16 and so on. Why this operation of multiplying a number by itself is called squaring? The reason is best grasped from the following picture.

A square with a side of length n can be visualized as comprising a grid of n×n smaller squares of size 1×1.

Triangular numbers owe their name to a similar construction, now of triangles. Actually we already used triangular numbers in the proof of Lemma 3 above. Triangular numbers are in the form 1, 3, 6, 10, 15, ... The general formula is that for every n the number N = n(n+1)/2 is triangular and describes the number of points arranged in a triangular shape with n points on a side as shown below.

Of course it needs to be proven that the total number of crosses arranged as in the diagram is given by the formula N = n(n+1)/2. However, we can observe that the number of crosses in every triangle equals the sum

1 + 2 + ... + n,

where n is the number of crosses on the side of the triangle. Thus, along the way, we are going to prove that

1 + 2 + ... + n = n(n+1)/2.

Another diagram will make this statement obvious

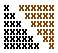
Indeed, two triangles, each with n crosses on the side, together form an n×(n+1) rectangle. You may question whether pointing to the diagram proves anything. No, of course by itself the diagram does not prove anything. But it does help to visualize and perhaps discern the proof. Indeed, we seek a formula for the sum of integers from 1 through n. This sum represents the number of crosses in a triangle. Two triangles of which one is rotated 180° form a rectangle, i.e. a shape in which all rows have the same number of crosses. Rows in the first triangle count crosses 1,2,3... in the increasing order whereas in the second we have rows with n, n-1, ... crosses in the decreasing order. Let us mimic this procedure in an algebraic manner.

First take two sums (one in increasing, another in decreasing order) (1 + ... + n) + (n + ... + 1). Now, regroup the terms by combining first terms in both sums, then second terms and so on:

[1+n] + [2+(n-1)] + [3+(n-2)] + ... + [(n-1)+2] + [n+1] = n(n+1)

Quite rigorously. Q.E.D.

It is obvious that all Euclid's perfect numbers are triangular.

References

1. J. H. Conway and R. K. Guy, The Book of Numbers, Springer-Verlag, NY, 1996.
2. R. Courant and H. Robbins, What is Mathematics?, Oxford University Press, 1966.
3. H. Davenport, The Higher Arithmetic, Harper&Brothers, NY.
4. W. Dunham, The Mathematical Universe, John Wiley & Sons, NY, 1994.
5. Encyclopædia Britannica
6. M. Gardner, Penrose Tiles To Trapdoor Ciphers, W.H.Freeman and Co., NY, 1989.
7. D. Knuth, Surreal Numbers, Addison-Wesley Publishing Co., 1974.
8. K. Kuratowski and A. Mostowski, Set Theory, North-Holand, Amsterdam, 1967.
9. M. Gardner, Time Travel and Other Mathematical Bewilderments, W.H.Freeman and Co., NY, 1988.
10. R. Rucker, Infinity and the Mind, Princeton University Press, Princeton, NJ, 1955
11. H. Schwerdtfeger, Geometry of Complex Numbers, Dover Publications, NY, 1979.
12. I.Stewart, Nature's Numbers, BasicBooks, 1995.

On the Web

1. Abstract Algebra OnLine
2. Ask Dr. Math
3. Eric's Treasure Trove of Mathematics
4. Triangular numbers (an online and iPod video by Julio de la Yncera)

Related material Read more...
	What's a number?
	Irrational number to an irrational power may be rational
	Bisector of an imaginary angle may be real
	Distances from the square root of 2
	Almost every integer has a digit 3 in it
	Pi is a remarkable number

|Contact| |Front page| |Contents| |Did you know?| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny