Bimedians in a Quadrilateral
What is this about?
A Mathematical Droodle

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

Bimedians in a Quadrilateral

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny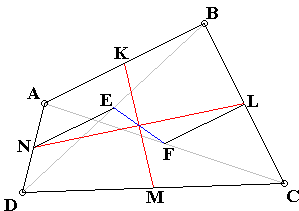

The applet illustrates the following statement:

In any quadrilateral, the lines joining the midpoints of the diagonals and those of the opposite sides are concurrent.

Indeed, from ΔABD, NE||AB and NE = AB/2. From ΔABC, FL||AB and FL = AB/2. Therefore, the quadrilateral ENFL is a parallelogram, whose diagonals are bisected by the point of intersection.

A similar argument applies to the quadrilateral EKFM. Since EF has only one midpoint, this is shared by the three lines.

It thus follows that the three lines EF, KM, and LN are concurrent and each is bisected by their common point. The three lines are known as the bimedians of the quadrilateral (and sometimes just medians), so that the statement could be formulated as

The three bimedians of any quadrilateral meet in a point by which they are divided in the ratio 1:1.

[F. G.-M., p. 50] notes that the problem was first posed and later solved in the first volume (1810-11) of the Annales de Gergonne.

The statement just proven admits a simple mechanical interpretation. Indeed, the point of intersection of the medians is nothing but the barycenter -- the center of gravity -- of a system of four equal weights (or material points) placed at the vertices of the quadrilateral. The statement just says that there are three ways to obtain the barycenter. The weights could be first combined two by two, which is possible in three ways, with the resulting 2-point system combined into a single point on the second step [Honsberger, p. 40, Wells, p. 161].

The median EF -- the line joining the midpoints of the diagonals of a quadrlateral -- is also known as its Newton's line [F. G.-M., p. 767]. The line appears in a theorem by Léon Anne and has significance for inscriptible quadrilaterals.

References

  1. C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, p. 108
  2. F. G.-M., Exercices de Géométrie, Jacques Gabay, 1991
  3. R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995
  4. C. W. Trigg, Mathematical Quickies, Dover, 1985, #198
  5. D. Wells, You Are a Mathematician, John Wiley & Sons, 1995

Barycenter and Barycentric Coordinates

  1. 3D Quadrilateral - a Coffin Problem
  2. Barycentric Coordinates
  3. Barycentric Coordinates: a Tool
  4. Barycentric Coordinates and Geometric Probability
  5. Ceva's Theorem
  6. Determinants, Area, and Barycentric Coordinates
  7. Maxwell Theorem via the Center of Gravity
  8. Bimedians in a Quadrilateral
  9. Simultaneous Generalization of the Theorems of Ceva and Menelaus
  10. Three glasses puzzle
  11. Van Obel Theorem and Barycentric Coordinates
  12. 1961 IMO, Problem 4. An exercise in barycentric coordinates
  13. Centroids in Polygon
  14. Center of Gravity and Motion of Material Points
  15. Isotomic Reciprocity
  16. An Affine Property of Barycenter
  17. Problem in Direct Similarity
  18. Circles in Barycentric Coordinates
  19. Barycenter of Cevian Triangle
  20. Concurrent Chords in a Circle, Equally Inclined

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

70571077