Newton's Theorem: What is it?
A Mathematical Droodle

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet
What if applet does not run?

Explanation

Newton's and Léon Anne's Theorems

The applet illustrates the following statement (Newton's theorem):

The center of the circle inscribed into a quadrilateral lies on the line joining the midpoints of the latter's diagonals.

The line is known as Newton's line. It exists for the quadrilaterals that are not parallelograms.

The statement is an immediate consequence of a theorem of Léon Anne:

Theorem (Pierre-Léon Anne, 1806-1850)

In any quadrilateral ABCD that is not a parallelogram, the locus of points O such that

Area( ΔAOB) + Area( ΔCOD) = Area( ΔBOC) + Area( ΔAOD)

is Newton's line of the quadrilateral.

Proof of Newton's Theorem

For any quadrilateral ABCD circumscribed around a circle AB + CD = BC + AD. (This is because two tangents from a point to a circle are equal. To derive the identity, consider four pairs of tangents -- one at each vertex of the quadrilateral.) Multiply that identity by R/2, where R is the radius of the circle, to obtain Area( ΔAOB) + Area( ΔCOD) = Area( ΔBOC) + Area( ΔAOD). By the theorem of Léon Anne, the proof is complete.

Proof 1 of the theorem of Léon Anne

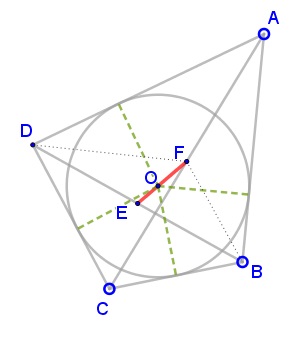
[F. G.-M, p. 767]. Since E is the midpoint of the diagonal BD, the lengths of the perpendiculars from BD onto the line EF are equal. Therefore, say, triangles BOF and DOF have equal areas. Similarly, Area( ΔAOF) = Area( ΔCOF). Further,

Area( ΔAOB) = Area( ΔAFB) + Area( ΔAOF) + Area( ΔBOF) and
Area( ΔDOC) = Area( ΔDFC) - Area( ΔCOF) - Area( ΔDOF).

Therefore

(1)

Area( ΔAOB) + Area( ΔCOD) = Area( ΔAFB) + Area( ΔCFD).

In the same manner,

Area( ΔAOD) = Area( ΔAFD) + Area( ΔDOF) - Area( ΔAOF) and
Area( ΔBOC) = Area( ΔBFC) - Area( ΔBOF) + Area( ΔCOF).

Wherefrom

(2)

Area( ΔAOD) + Area( ΔBOC) = Area( ΔAFD) + Area( ΔCFB).

But we know that Area( ΔAFB) = Area( ΔAFD) and also Area( ΔCFD) = Area( ΔCFB), which, combined with (1) and (2), yields

(3)

Area( ΔAOD) + Area( ΔBOC) = Area( ΔAOB) + Area( ΔCOD).

Proof 2 of the theorem of Léon Anne

[Honsberger, p. 174-175]

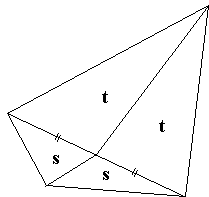
Since a median bisects the area of a triangle, the midpoints of the diagonals of the quadrilateral lie one the locus in question. An observation due to Basil Rannie makes it clear that the locus is a straight line.

The area of a triangle with a fixed base and a moving apex is the linear function of the Cartesian coordinates of the latter. If the apex is shared by two triangles, their total area is still a linear function of its coordinates. But the level curves of a linear function are straight lines.

References

C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010, pp. 116-118
F. G.-M., Exercices de Géométrie, Jacques Gabay, 1991
R. Honsberger, More Mathematical Morsels, MAA, 1991

40618382

Newton's Theorem: What is it? A Mathematical Droodle