Nagel Point on the Incircle in Isosceles Triangle
Source
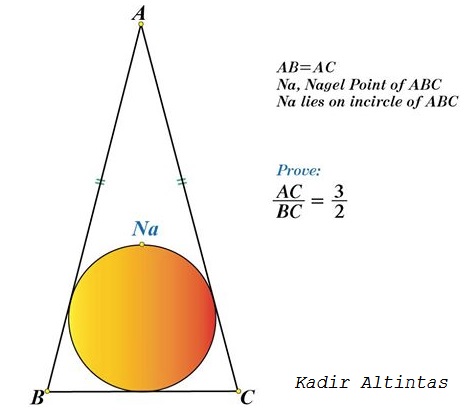
Problem
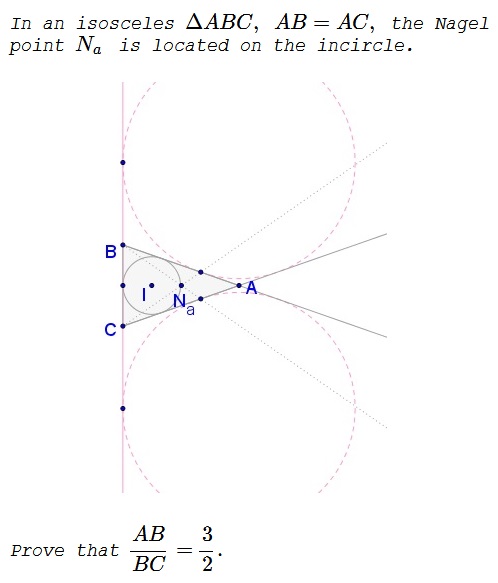
Solution 1
Due to the symmetry, $N_a\,$ is the "north pole" of the incircle. Thus, $2[\Delta ABC]=r(2b+a)=ah\,$ and $\displaystyle 2r=\frac{ha}{2b-a},\,$ implying $2b+a=4b-2a,\,$ i.e., $\displaystyle \frac{b}{a}=\frac{3}{2}.$
Solution 2
Nagel point lies on the incircle iff one side is one fouth of the perimeter. $BC=2a,\,$ $AC=AB=3a\,$ and the perimeter is $8a.\,$ It follows that $\displaystyle BC=\frac{1}{4}\,$ of the perimeter whereas $\displaystyle AB=\frac{3}{8}\,$ of the perimeter, thus, proving the claim.
Acknowledgment
The above problem - by Kadir Altintas - has been originally posted by Miguel Ochoa Sanchez at the Peru Geometrico facebook group. I am grateful to Leo Giugiuc for keeping me abreast via the CutTheKnotMath facebook page. Solution 1 is by Thanos Kalogerakis; Solution 2 is by Adir Altintas.
This is an example of the confiurations studied in the article SOME RELATIONS IN TRIANGLES WHOSE CENTERS ARE ON ITS INCIRCLE by LEONARD GIUGIUC AND ABDILKADIR ALTINTAS.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578511
