The Range of r/R in Triangle with Centroid on the Incircle
Problem
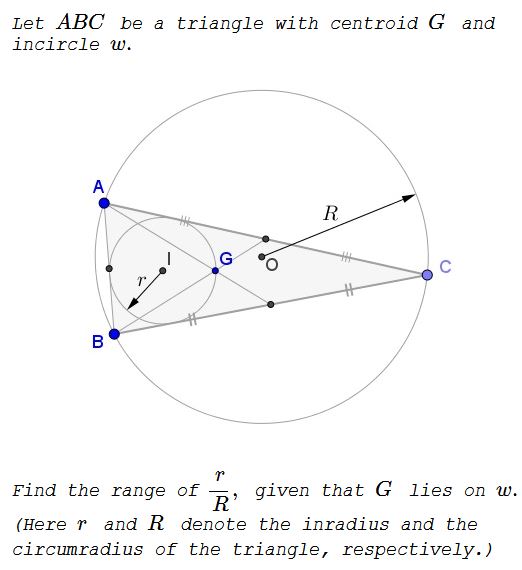
Solution
Let $I\,$ be the incenter of $\Delta ABC.\,$ We have
$\displaystyle \begin{align} 3\overset{\rightarrow}{GI} &= \overset{\rightarrow}{AI}+\overset{\rightarrow}{BI}+\overset{\rightarrow}{CI}&\Rightarrow\\ 9GI^2 &= AI^2+BI^2+CI^2+2(\overset{\rightarrow}{AI}\cdot\overset{\rightarrow}{BI}+\overset{\rightarrow}{BI}\cdot\overset{\rightarrow}{CI}+\overset{\rightarrow}{CI}\cdot\overset{\rightarrow}{AI})&\Rightarrow\\ 9GI^2 &= AI^2+BI^2+CI^2\\ &\qquad+(AI^2+BI^2-c^2+BI^2+CI^2-a^2+CI^2+AI^2-b^2)&\Rightarrow\\ 9GI^2 &= 3(AI^2+BI^2+CI^2)-(a^2+b^2+c^2)&\Rightarrow\\ GI^2&=\frac{AI^2+BI^2+CI^2}{3}-\frac{a^2+b^2+c^2}{9}. \end{align}$
Let $\displaystyle \frac{a+b+c}{2}=s.\,$ Denote $s-a=x,\,$ $s-b=y,\,$ $s-c=z.\,$ We get $a=y+z,\,$ $b=z+x,\,$ $c=x+y\,$ and $s=x+y+z.\,$ By Heron's formula, $[\Delta ABC]=\sqrt{xyz(x+y+z)}\,$ such that $\displaystyle r=\sqrt{\frac{xyz}{x+y+z}}\,$ and $\displaystyle R=\frac{(x+y)(y+z)(z+x)}{4\sqrt{xyz(x+y+z)}}.\,$ We also get
$\displaystyle \sin\frac{A}{2}=\sqrt{\frac{yz}{(z+x)(x+y)}},\,\sin\frac{B}{2}=\sqrt{\frac{zx}{(x+y)(y+z)}},\,\sin\frac{C}{2}=\sqrt{\frac{xy}{(y+z)(z+x)}}.$
Now, since $\displaystyle AI=\frac{\displaystyle r}{\displaystyle \sin\frac{A}{2}},\,$ $\displaystyle BI=\frac{\displaystyle r}{\displaystyle \sin\frac{A}{2}},\,$ $\displaystyle CI=\frac{\displaystyle r}{\displaystyle \sin\frac{C}{2}},\,$
$\displaystyle \begin{align} AI^2+BI^2+CI^2 &=\small{\frac{xyz}{x+y+z}\cdot\left[\frac{(z+x)(x+y)}{yz}+\frac{(x+y)(y+z)}{zx}+\frac{(y+z)(z+x)}{xy}\right]}\\ &=\frac{(x+y+z)^3-2(x+y+z)(xy+yz+zx)+3xyz}{x+y+z}. \end{align}$
But $a^2+b^2+c^2=2(x+y+z)^2-2(xy+yz+zx).\,$ With substitutions we obtain
$\displaystyle \begin{align} GI^2 &= \frac{(x+y+z)^3-4(x+y+z)(xy+yz+zx)+9xyz}{9(x+y+z)}\\ &= \frac{(x+y+z)^3-4(x+y+z)(xy+yz+zx)}{9(x+y+z)}+r^2.\\ \end{align}$
But, since $G\in w,\,$ $GI=r.\,$ Thus $(x+y+z)^2=4(xy+yz+zx).$
From here,
$\displaystyle \frac{r}{R}=\frac{xyz}{(x+y)(y+z)(z+x)}=\frac{\displaystyle 4xyz}{\displaystyle \frac{(x+y+z)^3}{4}-xyz}.$
WLOG, we may assume $x+y+z=6\,$ so that $\displaystyle \frac{4xyz}{54-xyz}.$
Consider the polynomial $P(t)=(t-x)(t-y)(t-z)\,$ for $t\ge 0.\,$ $P(t)=t^3-6t+9t-xyz,\,$ $P'(t)=3(t^2-4t+3)=3(t-1)(t-3).\,$ It follows that $P\,$ is strictly increasing on $[0,1],\,$ and $[3,\infty),\,$ and strictly decreasing on $[1,3].$
Thus, $P(0)=-xyz\lt 0,\,$ $P(1)=4-xyz,\,$ $P(3)=-xyz\lt 0,\,$ and $P(\infty)=\infty\gt 0.$
Since $P\,$ has three positive real roots, we deduce from Rolle's theorem that $4-xyz\ge 0,\,$ i.e., $xyz\le 4.\,$ Further, with $(x,y,z)=(1,1,4),\,$ $xyz=4,\,$ implying that the range of $xyz\,$ is $(0,4].\,$ But the function $\displaystyle f(t)=\frac{4t}{54-t}\,$ is strictly increasing on $(0,4]\,$ so that $\displaystyle f\bigg((0,4]\bigg)=\left(0,\frac{8}{25}\right].\,$ This means that the range of $\displaystyle \frac{r}{R}\,$ is the interval $\displaystyle \left(0,\frac{8}{25}\right].$
Acknowledgment
The above problem and the solution - by Leonard Giugiuc,Kadir Altintas (Turkey) and Marian Dinca (Romania) - have been kindly communicated to me by Leo Giugiuc.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73572723
