Centroid on the Incircle in Isosceles Triangle

Source

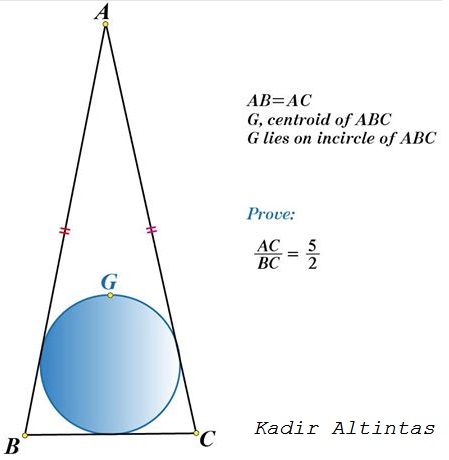
Centroid on the Incircle in Isosceles Triangle, source

Problem

In an isosceles $\Delta ABC,\,$ $AB=AC,\,$ the centroid $G\,$ is located on the incircle.

Centroid on the Incircle in Isosceles Triangle, Illustration

Prove that $\displaystyle \frac{AB}{BC}=\frac{5}{2}.$

Solution 1

Due to the symmetry, $G\,$ is the "north pole" of the incircle. Thus, $\displaystyle 2r=\frac{h}{3}\,$ and $2[\Delta ABC]=r(2b+a)=ah,\,$ implying $2b+a=6a,\,$ i.e. $\displaystyle \frac{b}{a}=\frac{5}{2}.$

Solution 2

We know that, when $G\,$ is on the incircle,

$\displaystyle 5(a^2+b^2+c^2)=6(ab+bc+ca).$

With $b=c,\,$ this becomes $5(a^2+2b^2)=6(b^2+2ab),\,$ i.e., $5a^2-12ab+4b^2=0,\,$ with two solutions $2b=a\,$ and $2b=5a.\,$ The first one is impossible as it violates the triangle inequality. The remaining one solves the problem.

Acknowledgment

The above problem - by Kadir Altintas - has been originally posted by Miguel Ochoa Sanchez at the Peru Geometrico facebook group. I am grateful to Leo Giugiuc for keeping me abreast via the CutTheKnotMath facebook page. Solution 1 is by Thanos Kalogerakis; Solution 2 is by Adir Altintas.

Related material Read more...

	R and r When G on Incircle
	The Range of r/R in Triangle with Centroid on the Incircle
	Centroid on the Incircle in Right Triangle
	Nagel Point on the Incircle in Isosceles Triangle
	Nagel Point and Centroid on Adjacent Isosceles Triangles

71925294