Centroid on the Incircle in Right Triangle
Source
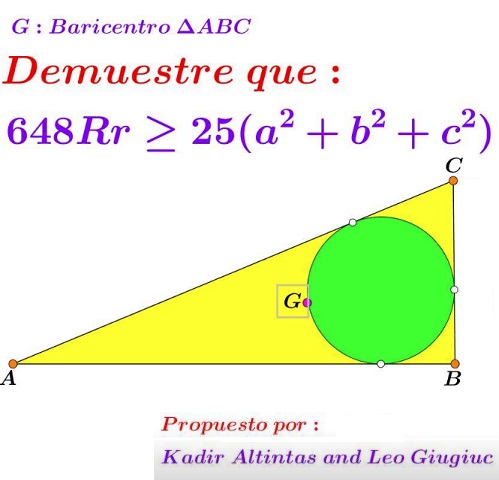
Problem
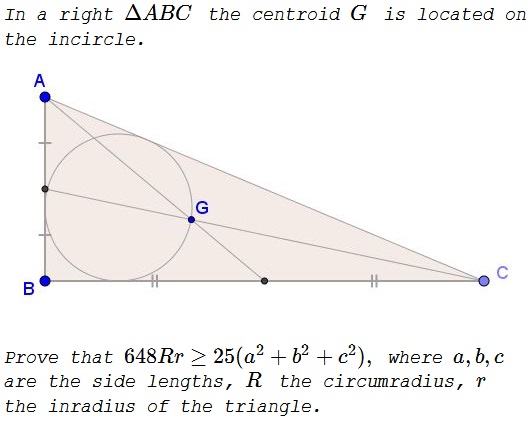
Solution
We know that
$\displaystyle GI^2=\frac{1}{18}(a^2+b^2+c^2-24Rr+12r^2),$
Since $IG=r,\,$ we derive $a^2+b^2+c^2=6r^2+24Rr,\,$ implying that what we need to prove is
$\displaystyle 648Rr\ge 25(6r^2+24Rr),$
or, equivalently, $48Rr\ge 25\cdot 6r^2,\,$ i.e., $8R\ge 25r,\,$ which is a well-known inequality.
Acknowledgment
The above problem - by Kadir Altintas and Leo Giugiuc - has been originally posted by Miguel Ochoa Sanchez at the Peru Geometrico facebook group. I am grateful to Leo Giugiuc for keeping me abreast via the CutTheKnotMath facebook page. The solution is by Marian Dinca.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558827
